Метод ГАУССА решения систем линейных уравнений и его модификации
Методические указания к выполнению лабораторных работ по дисциплине Численные методы для студентов направлений (специальностей) 010100 Математика, 050100 Педагогическое образование (050101, 050202)
Курган 2014
Кафедра: «Математического анализа»
Дисциплина: «Численные методы»
010100 Математика,
050100 Педагогическое образование (050101, 050202)
Составили: канд. пед. наук, доц. Т.Н. Михащенко (теоретическая часть,
варианты заданий, общая редакция);
студент Лобков В.Ю. (примеры расчета, набор текста).
Введение
Известно, что почти 75% всех расчётных математических задач приходится на решение систем линейных алгебраических уравнений, так как математические модели тех или иных явлений или процессов или сразу строятся как линейные, или сводятся к ним. Поэтому не трудно переоценить роль, которую играет выбор эффективного способа решения системы линейных уравнений. Современная вычислительная математика располагает большим арсеналом методов, а математическое обеспечение ЭВМ – многими пакетами прикладных программ, позволяющих решать различные линейные системы.
Целью данного методического пособия является ознакомление студентов с различными модификациями самого распространенного метода решения систем линейных уравнений – метода Гаусса.
В пособии содержатся методические рекомендации по организации вычислений, задание для лабораторной работы по теме «Методы решения систем линейных уравнений», все схемы снабжены подробными инструкциями по их применению и алгоритмизированы для программирования на ЭВМ.
На выбор студенту предлагается несколько модификаций проведения и оформления вычислений: полная и компактная схемы Гаусса, модификация Краута-Дулитла, схема Гаусса с выбором главного элемента.
1. Компактная схема Гаусса
Компактная схема Гаусса дает экономный способ записи вычислений и полностью соответствует традиционному методу Гаусса, изучаемому в курсе алгебры.
Суть метода Гаусса….
Рассмотрим порядок составления схемы для системы четырёх уравнений с четырьмя неизвестными. Все результаты вычислений будем записывать в одну таблицу (таблица 1).
Таблица 1
Компактная схема Гаусса
| i | ai 1 | ai 2 | ai 3 | ai 4 | ai 5 | ai 6 | 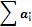 | 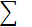 | |
| I | a 11 | a 12 | a 13 | a 14 | a 15 | a 1 j = a 16 | |||
| a 21 | a 22 | a 23 | a 24 | a 25 | a 2 j = a 26 | ||||
| a 31 | a 32 | a 33 | a 34 | a 35 | a 3 j = a 36 | ||||
| a 41 | a 42 | a 43 | a 44 | a 45 | a 4 j = a 46 | ||||
| b 12 | b 13 | b 14 | b 15 | a 16 / a 11= b 16 | |||||
| II | a 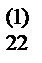 | a 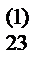 | a 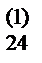 | a 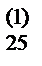 | a 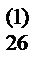 | ||||
a 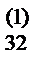 | a 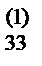 | a 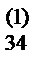 | a 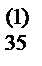 | a 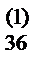 | |||||
a 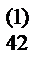 | a 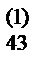 | a 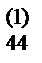 | a 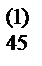 | a 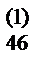 | |||||
b 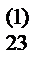 | b 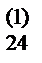 | b 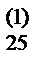 | a 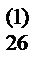 /a /a 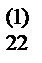 = b = b 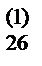 | ||||||
| III | a 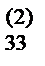 | a 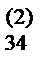 | a 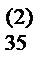 | a 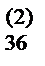 | |||||
a 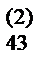 | a 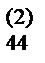 | a 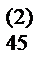 | a 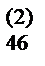 | ||||||
b 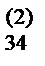 | b 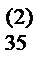 | a 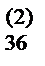 / a / a 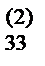 = b = b 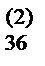 | |||||||
| IV | a 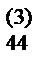 | a 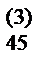 | a 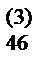 | ||||||
| V | x4 | ||||||||
| x3 | |||||||||
| x2 | |||||||||
| x1 |
Порядок заполнения таблицы (прямой ход):
1) Записываем коэффициенты системы в четырёх строках и пяти столбцах раздела I (табл. 1).
2) Суммируем все коэффициенты по строке и записываем сумму в столбце 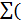 столбец контроля), т.е. a 16=
столбец контроля), т.е. a 16= 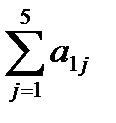 .
.
3) Делим все числа, стоящие в первой строке, на ведущий элемент a11 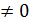 и результаты b 1j= a 1j / a 11 записываем в пятой строке раздела I.
и результаты b 1j= a 1j / a 11 записываем в пятой строке раздела I.
4) Вычисляем 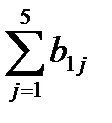 и делаем проверку. Если вычисления ведутся постоянным знаком после запятой, то числа b 16 и
и делаем проверку. Если вычисления ведутся постоянным знаком после запятой, то числа b 16 и 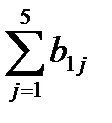 не должны отличаться более чем на единицу последнего разряда. В противном случае следует проверить действия пункта 3.
не должны отличаться более чем на единицу последнего разряда. В противном случае следует проверить действия пункта 3.
5) Вычисляем коэффициенты a 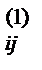 (i =2,3,4; j= 2,3,4,5,6)по формуле
(i =2,3,4; j= 2,3,4,5,6)по формуле
a 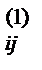 =aij–ai1b1j. Результаты записываем в первые три строки раздела II.
=aij–ai1b1j. Результаты записываем в первые три строки раздела II.
6) Осуществляем контроль. Сумма элементов каждой строки 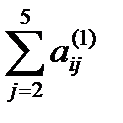 (i =2,3,4) не должна отличаться от a
(i =2,3,4) не должна отличаться от a 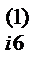 более чем на единицу последнего разряда.
более чем на единицу последнего разряда.
7) Делим все элементы первой строки раздела II на a 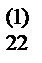
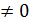 , результаты записываем в четвёртой строке раздела II. Осуществляем контроль.
, результаты записываем в четвёртой строке раздела II. Осуществляем контроль.
8) Вычисляем a 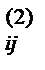 , a
, a 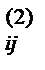 = a
= a 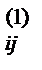 – a
– a 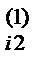 b
b 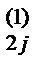 , (i =3,4; j =3,4,5,6). Осуществляем контроль.
, (i =3,4; j =3,4,5,6). Осуществляем контроль.
9) Делим элементы первой строки раздела III на a 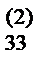 и находим числа b
и находим числа b 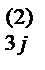 =a
=a 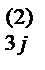 /a
/a 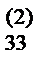 . Все результаты записываем в третьей строке раздела III. Осуществляем контроль.
. Все результаты записываем в третьей строке раздела III. Осуществляем контроль.
10) Вычисляем a 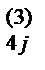 = a
= a 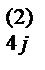 - a
- a 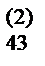 b
b 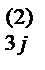 . Результаты записываем в разделе IV.
. Результаты записываем в разделе IV.
Обратный ход:
11) В разделе V записываем единицы, как это указано в табл. 1, вычисляем x4= a 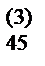 / a
/ a 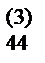 .
.
12) Для вычисления значений x3,x2,x1 используются лишь строки разделов I, II, III, содержащие единицы (отмеченные строки). Так для вычисления x3 умножаем x4 на b 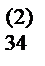 и получившееся произведение вычитаем из b
и получившееся произведение вычитаем из b 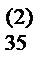 . При этом единицы, расставленные в разделе V, помогают находить для x i (i= 3,2,1) соответствующие коэффициенты в отмеченных строках. Таким образом,
. При этом единицы, расставленные в разделе V, помогают находить для x i (i= 3,2,1) соответствующие коэффициенты в отмеченных строках. Таким образом,
x3= b 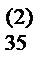 - b
- b 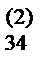 x4.
x4.
13) Вычисляем x2, и затем x1, для чего используем элементы отмеченной строки раздела II: x2= b 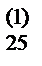 - b
- b 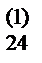 x4- b
x4- b 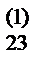 x3,
x3,
x1= b 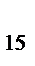 - b
- b 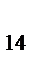 x4 - b
x4 - b 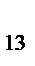 x3 - b
x3 - b 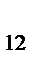 x2.
x2.
Компактная схема Гаусса оказывается особенно выгодной при одновременном решении нескольких систем, отличающихся лишь столбцами свободных членов, при вычислении обратной матрицы.
Решим с помощью компактной схемы Гаусса систему уравнений, все вычисления занесем в таблицу (табл.2): 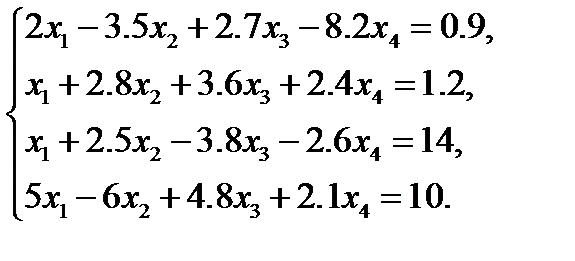
Следуя порядку действий, указанному в параграфе 1, получаем значения неизвестных: x4=0,068976; х3=-1,815417; x2=0,964032; х1=4,870672.
Проверка показывает, с какой точностью получен результат, погрешность вычислений не превосходит соответственно 0,0000029; 0,0000028; 0,000001; 0,000016 в первом, втором, третьем и четвертом уравнениях.
Таблица 2
| i | x1 | x2 | x3 | x4 | Свободные члены | | | |
| I | -3,5 | 2,7 | -8,2 | 0,9 | -6,1 | |||
| 2,8 | 3,6 | 2,4 | 1,2 | |||||
| 2,5 | -3,8 | -2,6 | 11,1 | |||||
| -6 | 4,8 | 2,1 | 15,9 | |||||
| -1,75 | 1,35 | -4,1 | 0,45 | -3,05 | -3,05 | |||
| II | 4,55 | 2,25 | 6,5 | 0,75 | 14,05 | 14,05 | ||
| 4,25 | -5,15 | 1,5 | 13,55 | 14,15 | 14,15 | |||
| 2,75 | -1,95 | 22,6 | 7,75 | 31,15 | 31,15 | |||
| 0,494505 | 1,428571 | 0,164835 | 3,087912 | 3,087912 | ||||
| III | -7,251648 | -4,571429 | 12,849451 | 1,026374 | 1,026374 | |||
| -3,30989 | 18,671429 | 7,296703 | 22,658242 | 22,658242 | ||||
| 0,630399 | -1,771935 | -0,141537 | -0,141537 | |||||
| IV | 20,757978 | 1,431793 | 22,189771 | 22,189771 | ||||
| 0,068976 | 1,068976 | 1,068976 | ||||||
| V | 0,068976 | 0,0000029 | ||||||
| -1,815417 | 0,0000028 | |||||||
| 0,964032 | 0,000001 | |||||||
| 4,870672 | 0,000016 |
2. Модификация Краута – Дулитла
Если учесть некоторые возможности клавишных вычислительных машин, то можно составить схему вычислений, позволяющую ещё больше сократить записи промежуточных результатов по сравнению с компактной схемой Гаусса.
Порядок заполнения таблицы, прямой ход:
1) Записываем коэффициенты системы aij для i =1,2,3,4; j =1,2,3,4,5 в разделе I (табл.3).
2) Суммируем коэффициенты по каждой строке и результаты заносим в столбец в качестве ai 6 (i =1,2,3,4).
3) При i= 2,3,4 находим числа m i 1= ai 1 / a 11 и записываем их в разделе II.
4) При j= 2,3,4,5,6 вычисляем коэффициенты a 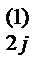 по формуле a
по формуле a 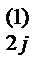 = a 2 j – m 21 а 1 j и записываем их вразделе III.
= a 2 j – m 21 а 1 j и записываем их вразделе III.
5) Контроль: сумма 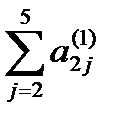 не должна отличаться от a
не должна отличаться от a 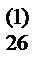 более чем на единицу последнего разряда.
более чем на единицу последнего разряда.
6) При i =3,4 находим числа тi 2по формуле тi 2=(ai 2– mi 1 a 12)/ a 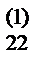 и заносим в раздел IV.
и заносим в раздел IV.
7) При j =3,4,5,6 вычисляем коэффициенты a 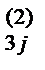 по формуле
по формуле
a 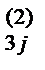 = a 3 j – m 31 a 1 j – m 32 a
= a 3 j – m 31 a 1 j – m 32 a 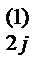 и записываем в раздел V.
и записываем в раздел V.
8) Находим число m 43=(a 43 – m 41 а 13 – m 42 a 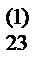 )/ a
)/ a 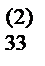 и записываем его в раздел VI.
и записываем его в раздел VI.
9) При j =4,5,6 находим коэффициенты a 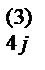 по формуле a
по формуле a 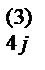 = a 4 j – m 41 a 1 j – m 42 a
= a 4 j – m 41 a 1 j – m 42 a 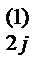 – m 43 a
– m 43 a 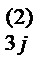 и записываем в раздел VII.
и записываем в раздел VII.
10) Контроль: сравниваем сумму a  + a
+ a 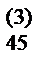 с числом a
с числом a 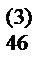 .
.
Обратный ход осуществляется аналогично компактной схеме Гаусса. Находим неизвестные x4, x3, x2, x1 по формулам: a 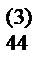 x4= a
x4= a 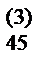 , a
, a 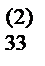 x3+ a
x3+ a 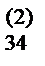 x4= a
x4= a 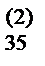 , a
, a 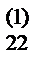 x2+ a
x2+ a 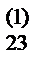 x3+ a
x3+ a 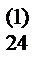 x4= a
x4= a 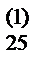 , a 11x1+ a 12x2+ a 13x3+ a 14x4= a 15. Вычисления по этим формулам ведутся без промежуточных записей. Результаты записываются в разделе VIII таблицы.
, a 11x1+ a 12x2+ a 13x3+ a 14x4= a 15. Вычисления по этим формулам ведутся без промежуточных записей. Результаты записываются в разделе VIII таблицы.
Таблица 3
 2015-03-22
2015-03-22 2984
2984







