Краткая теория. 1. Постановка задачи. Производится n наблюдений ,, переменных х и у

1. Постановка задачи. Производится n наблюдений 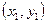,..., 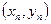переменных х и у. Предполагая, что между х и у существует зависимость вида 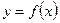,найти значения параметров а и b,наилучшим образом согласованные с экспериментальными данными.

Согласно методу наименьших квадратов параметры функции 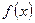следует выбирать так, чтобы сумма квадратов невязок 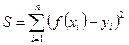(15.14)

была наименьшей.

2. Если 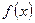– линейная функция, т.е. 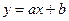, то 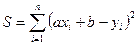, а неизвестные параметры а и b определяются из системы нормальных уравнений:

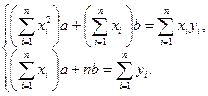(15.15)

3. Если 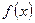– квадратичная функция, т.е. 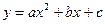, то 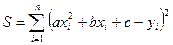, а неизвестные параметры а, b, с определяются из системы нормальных уравнений:

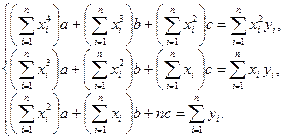(15.16)

15.88. Имеются следующие данные о величине пробега автомобиля х (тыс. км) и у – расходе масла (л/тыс. км):

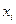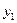	0,2	0,5	0,8	1,1	1,3

Полагая, что между переменными х и у существует линейная зависимость, найти эмпирическую формулу 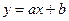методом наименьших квадратов.

Решение. Найдем необходимые для решения суммы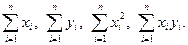

Промежуточные вычисления представлены в таблице:

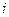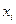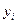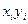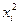		0,2
		0,5
		0,8
		1,1
		1,3
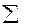		3,9

Система нормальных уравнений (15.15) имеет вид:

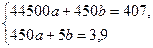
Ее решения 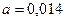, 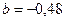. Таким образом, линейная зависимость имеет вид: .

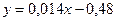15.89. Имеется шесть измерений пары переменных 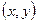, результаты которых приведены в таблице:

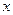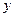	0,2	0,3	1,0	1,2

Методом наименьших квадратов построить линейную зависимость 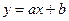. Сравнить полученную зависимость с зависимостью .

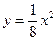Решение. Аналогично задаче 15.88 найдем уравнение линейной зависимости: .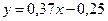

Сравним величины 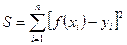для найденной линейной зависимости и зависимости 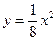. Промежуточные вычисления представим в таблице:

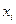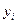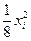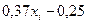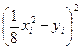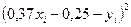		0,2	0,125	0,12	0,005625	0,0064
		0,3	0,5	0,49	0,040000	0,0361
		1,0	1,125	0,76	0,015625	0,0576
		1,2		1,23	0,640000	0,0009
					0,701250	0,1010

Как видно 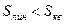, следовательно, линейная зависимость предпочтительнее.

15.90. Имеются следующие данные о расходах на рекламу х (тыс. усл, ед.) и сбыте продукции у (тыс. ед.):

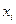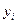	1,6	4,0	7,4	12,0	18,0

Предполагая, что между переменными х и у существует квадратичная зависимость вида 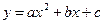, найти значения параметров а, b, с методом наименьших квадратов.

Решение. Найдем необходимые для решения суммы

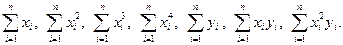
Вычисления приведены в таблице:

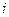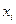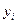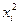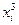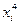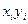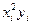		1,6				1,6	1,6
		4,0				8,0	16,0
		7,4				22,2	66,6
		12,0				48,0	196,0
		18,0				90,0	450,0
		43,0				169,8	730,2

Система нормальных уравнений (15.16) имеет вид:

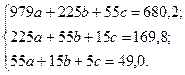
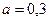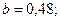
Ее решение ; 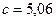. Таким образом, искомая зависимость имеет вид: .

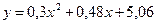Имеются следующие данные о переменных х и у. Предполагая, что между

х и у существует линейная зависимость, найти эмпирическую формулу 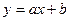методом наименьших квадратов:

15.91. х -цена на товар (усл.ед.);у –уровень продаж (тыс.ед.):

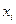	3,0	4,0	5,0	6,0	7,0

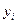15.92. х -уровень потребления электроэнергии на предприятии (млн кВт. ч);у –себестоимость единицы продукции:

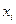	1,2	1,3	1,4	1,5	1,6
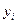	20,0	18,8	18,2	18,1	18,0

15.93. х -мощность двигателя (л.с.);у –средний срок его эксплуатации (мес.):

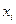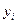По экспериментальным данным построить методом наименьших квадратов

линейную эмпирическую зависимость 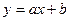. Сравнить полученную зависимость с альтернативной и определить, какая из них лучше соответствует экспериментальным данным:

15.94.

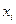		2,5		3,5
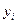	4,2	5,5	6,9		9,5

Альтернативная зависимость .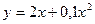

15.95.

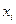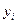	1,0	1,4	1,7	2,0	2,2

Альтернативная зависимость .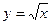

15.96.

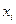	1,0	1,5	2,0	2,5	3,0
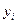	0,50	0,30	0,25	0,18	0,12

Альтернативная зависимость .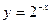

15.97. Имеютсяследующие экспериментальные данные о количестве единиц произведенной продукции х и издержках у (тыс.усл.ед.):

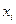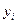	2,0	5,9	12,0	20,0	30,0

Функция издержек ищется в виде 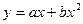. Определить параметры а и b функции методом наименьших квадратов.

15.98. Имеютсяследующие экспериментальные данные о количестве произведенного товара х (тыс.ед.) и количестве реализованного товара К(х) (тыс.ед.):

Зависимость ищется в виде 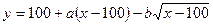. Найти ее параметры а и b функции методом наименьших квадратов.

Указание. Для решения задач 15.97 – 15.98 вначале необходимо получить свою систему нормальных уравнений, исходя из равенств: 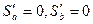, где S определяется по формуле (15.14).

15.5. Двойные интегралы