Первый способ. При условии 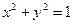 имеем
имеем 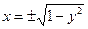 и получаем две функции одной переменной
и получаем две функции одной переменной 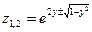 ;
; 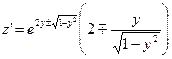 .
.
Критические точки задаются равенствами 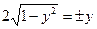 , т.е.
, т.е. 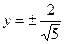 . Таким образом, имеем две критические точки
. Таким образом, имеем две критические точки 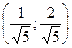 и
и 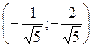 .
.
Легко проверить, что 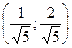 – точка максимума и
– точка максимума и 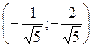 – точка минимума.
– точка минимума.
Второй способ. Функция Лагранжа (15.8) имеет вид:
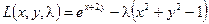 . (15.8)
. (15.8)
Приравнивая ее частные производные к нулю, получаем систему:
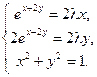
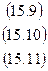
Из уравнений (15.9) и (15.10) находим 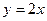 ,подставляя в (15.11), получаем два решения
,подставляя в (15.11), получаем два решения 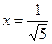 ,
, 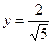 и
и 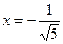 ,
, 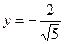 . Таким образом, получаем те же две критические точки
. Таким образом, получаем те же две критические точки 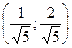 – точку максимума и
– точку максимума и 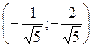 – точку минимума.
– точку минимума.
Исследовать функции на экстремум:
15.62. 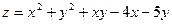 . 15.63.
. 15.63. 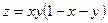 . 15.64.
. 15.64. 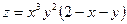 .
.
15.65. 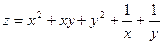 . 15.66.
. 15.66. 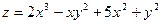 . 15.65.
. 15.65. 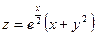 .
.
Найти наибольшее и наименьшее значения функции в областях, задаваемых неравенствами:
15.76. 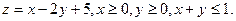 15.77.
15.77. 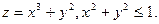 .
.
15. 78. 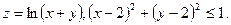
15. 79. Из всех прямоугольных параллелепипедов, имеющих данную сумму длин ребер а, найти параллелепипед, имеющий наибольший объем.
Исследовать функции на условный экстремум:
15.80. 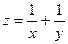 при х + у = 2. 15.81.
при х + у = 2. 15.81. 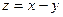 при
при 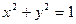 .
.
15.82. 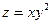 при х + 2у = 4. 15.83.
при х + 2у = 4. 15.83. 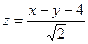 при
при 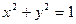 .
.
 2015-03-22
2015-03-22 1013
1013
