1. Находим частные производные:
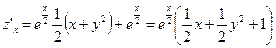 ;
; 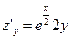 .
.
2. Находим критические точки функции из системы
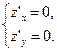
Получаем 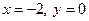 , т.е.
, т.е. 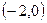 – единственная критическая точка.
– единственная критическая точка.
3. Находим частные производные второго порядка:
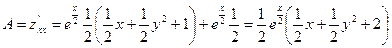 ;
;
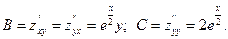
Имеем 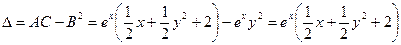 .
.
В точке (–2; 0) имеем 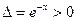 ,
, 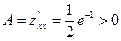 . Таким образом, (– 2; 0) – точка минимума.
. Таким образом, (– 2; 0) – точка минимума.
4. Находим минимум функции 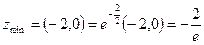 .
.
15.57. Найти экстремумы функции 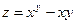 .
.
Решение. 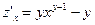 ;
; 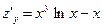 . Легко проверить, что равенство
. Легко проверить, что равенство 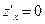 выполняется в трех случаях: при х = 1, при у = 0ипри
выполняется в трех случаях: при х = 1, при у = 0ипри 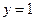 . В первых двух случаях уравнение
. В первых двух случаях уравнение 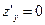 не имеет решений, так что единственное решение системы
не имеет решений, так что единственное решение системы
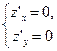
есть 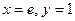 , т.е.критическая точка (е; 1) – единственная. Имеем
, т.е.критическая точка (е; 1) – единственная. Имеем
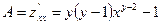 ;
; 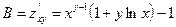 ;
; 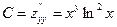 .
.
В точке 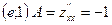 ;
; 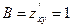 ;
; 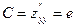 .
.
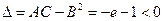 , так что функция экстремумов не имеет. Такая точка (е; 1) есть седловая точка.
, так что функция экстремумов не имеет. Такая точка (е; 1) есть седловая точка.
15.58. Найти экстремумы функции 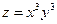 .
.
Решение. 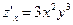 ;
; 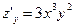 . Очевидно, (0; 0) – единственная критическая точка:
. Очевидно, (0; 0) – единственная критическая точка: 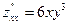 ;
; 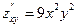 ;
; 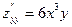 . Очевидно, в точке (0; 0)
. Очевидно, в точке (0; 0) 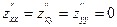 , т.е.
, т.е. 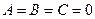 ,
, 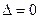 , и вопрос об экстремуме остается открытым, так что требуется дополнительное исследование.
, и вопрос об экстремуме остается открытым, так что требуется дополнительное исследование.
Очевидно, в любой окрестности точки (0; 0) функция может принимать и положительные, и отрицательные значения (например, в точке (1; 1) z = 1 > 0, а в точке
(– 1; 1) z = – 1 < 0); в самой же точке (0; 0) функция равна нулю. Таким образом, ни в какой своей окрестности точка (0; 0) не является ни точкой максимального, ни точкой минимального значения, т.е. функция экстремумов не имеет.
|
|
|
15.59. Найти наибольшее и наименьшее значение функции 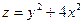 на круге
на круге 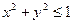 .
.
Решение. Критическая точка 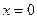 ,
, 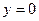 – единственная и расположена внутри круга
– единственная и расположена внутри круга  . На границе круга
. На границе круга 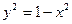 и
и 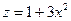 ,где
,где 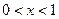 . Таким образом, на границе имеем
. Таким образом, на границе имеем 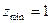 ,
, 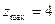 . Следовательно, наименьшее значение
. Следовательно, наименьшее значение 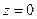 принимается внутри круга, наибольшее
принимается внутри круга, наибольшее 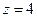 – на его границе.
– на его границе.
15.60. Найти экстремумы функции 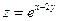 при условии, что
при условии, что 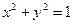 .
.
 2015-03-22
2015-03-22 544
544








