1. Точка 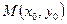 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции 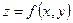 если существует окрестность точки М, такая, что для всех точек
если существует окрестность точки М, такая, что для всех точек 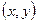 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство
 .
.
2. Если в точке максимума или минимума обе частные производные существуют и непрерывны, то они равны нулю в этой точке (необходимое условие экстремума).
3. Если в точке 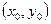 обе частные производные обращаются в нуль, то характер этой точки определяется величиной
обе частные производные обращаются в нуль, то характер этой точки определяется величиной 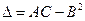 , где
, где 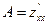 ,
, 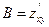 ,
, 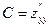 .
.
При 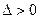 имеется экстремум (максимум при
имеется экстремум (максимум при 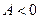 и минимум при
и минимум при 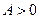 ).
).
При 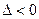 функция в данной точке не имеет экстремума.
функция в данной точке не имеет экстремума.
При 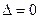 вопрос о наличии экстремума остается открытым (достаточное условие экстремума).
вопрос о наличии экстремума остается открытым (достаточное условие экстремума).
4. Наибольшее (наименьшее) значение функции (глобальный максимум (минимум)) 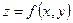 определяется как наибольшее (наименьшее) значение функции в замкнутой области из ее значений в критических точках внутри области и на ее границе.
определяется как наибольшее (наименьшее) значение функции в замкнутой области из ее значений в критических точках внутри области и на ее границе.
5. Точка 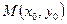 называется точкой условного максимума (минимума) функции
называется точкой условного максимума (минимума) функции 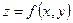 при условии
при условии 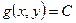 если, существует такая окрестность этой точки, что во всех точках (х, у) из этой окрестности, удовлетворяющих условию g (x, у) = С, выполняется неравенство
если, существует такая окрестность этой точки, что во всех точках (х, у) из этой окрестности, удовлетворяющих условию g (x, у) = С, выполняется неравенство  .
.
Уравнение 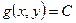 называется уравнением связи. Точка условного экстремума является точкой экстремума функции
называется уравнением связи. Точка условного экстремума является точкой экстремума функции 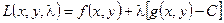 . Функция L называется функцией Лагранжа, а
. Функция L называется функцией Лагранжа, а 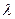 , – множителем Лагранжа.
, – множителем Лагранжа. 
6. При исследовании функции на экстремум рекомендуется пользоваться следующей схемой:
1. Найти частные производные 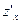 и
и 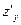
2. Решить систему уравнений 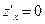 и
и 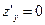 и найти критические точки функции.
и найти критические точки функции.
3. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
4. Найти экстремумы (экстремальные значения) функции.
15.56. Найти экстремумы функции 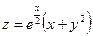 .
.
 2015-03-22
2015-03-22 671
671








