1. Приращение 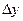 дифференцируемой функции
дифференцируемой функции 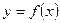 может быть представлено в виде:
может быть представлено в виде: 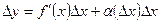 , (9.1)
, (9.1)
где 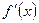 - производная функции
- производная функции 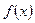 ;
; 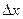 - приращение независимой переменной;
- приращение независимой переменной; 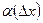 - бесконечно малая величина.
- бесконечно малая величина.
2. Дифференциалом (первого порядка) функции 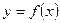 называется главная, линейная относительно
называется главная, линейная относительно 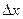 часть приращения функции, равная произведению производной на приращение независимой переменной:
часть приращения функции, равная произведению производной на приращение независимой переменной:
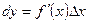 (9.2)
(9.2)
Дифференциал независимой переменной равен приращению этой переменной:
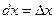 (9.3)
(9.3)
Поэтому дифференциал функции
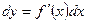 (9.4)
(9.4)
3. Свойства дифференциала:
1) 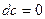 , где с = const. 2)
, где с = const. 2) 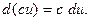
3) 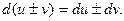 4)
4) 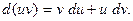 (9.5)
(9.5)
5) 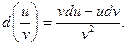 6)
6) 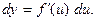
4. Применение дифференциала в приближенных вычислениях.
При достаточно малых значениях ∆ х приращение функции ∆ у ≈ dy, т.е.
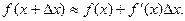 (9.6)
(9.6)
Чем меньше значение ∆ х, тем точнее формула (9.6).
Если аргумент х вычислен с относительной погрешностью 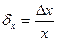 , то, функция
, то, функция 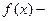 с относительной погрешностью
с относительной погрешностью 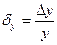 , определяемой по формуле
, определяемой по формуле
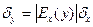 , (9.7)
, (9.7)
где 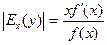 - эластичность функции (по абсолютной величине).
- эластичность функции (по абсолютной величине).
5. Дифференциалы высших порядков.
Дифференциалом второго порядка (или вторым дифференциалом) d2y функции
y = f (x) называется дифференциал от дифференциала первого порядка этой функции, т.е.
d 2 y = d (dy). (9.8)
Дифференциалом n-го порядка dny называется дифференциал от дифференциала
(n – 1) –го порядка этой функции, т.е. d n y = d (dn -1 y). (9.9)
9.1. Найти дифференциал функции y = x 2 + x + 1 в точке х = 2 двумя способами:
а) выделяя линейную относительно ∆ х часть приращения функции ∆ у;
б) по формуле dy = f′ (x) dx.
 2015-03-22
2015-03-22 1617
1617
