1. Прямая l называется асимптотой графика функции у = ƒ(х), если расстояние от точки (х, ƒ(х)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Асимптоты бывают вертикальными, горизонтальными и наклонными.
2. Прямая х = xо является вертикальной асимптотой графика
функции у= ƒ(х), если хотя бы один из пределов 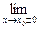 ƒ(х) (правосторонний или левосторонний) равен
ƒ(х) (правосторонний или левосторонний) равен 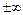 .
.
Прямая х = xо может быть вертикальной асимптотой функции y = ƒ(х) в том случае, если xо – точка разрыва или граничная точка области определения.
3. Прямая у = b является горизонтальной асимптотой, если lim ƒ(х) = b.
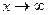
Если lim ƒ(х) = b, то у = b — правосторонняя горизонтальная асимптота,
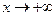
если lim ƒ(х) = b, то у = b — левосторонняя горизонтальная асимптота.
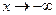
4. Если 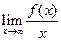 = k
= k 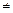 0 и
0 и 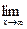
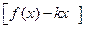 = b, то прямая y = kx + b является наклонной асимптотой графика функции y = ƒ(х).
= b, то прямая y = kx + b является наклонной асимптотой графика функции y = ƒ(х).
5. Общая схема исследования функций и построения графиков:
1) найти область определения функции;
2) исследовать функцию на четность – нечетность;
3) найти вертикальные асимптоты;
4) исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты;
5) найти экстремумы и интервалы монотонности функции;
6) найти интервалы выпуклости функции и точки перегиба;
7) найти точки пересечения графика функции с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Исследование функции проводится одновременно с построением графиков.
8.94. Исследовать функцию 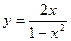 и построить ее график.
и построить ее график.
Решение:
1. Область определения 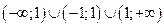 . Точки
. Точки 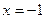 и
и 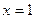 – точки разрыва функции.
– точки разрыва функции.
2. ƒ(- х) = -ƒ(х), т.е. функция нечетная; её график симметричен относительно начала координат и достаточно провести исследования функции на интервале 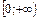 .
.
3. 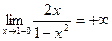 ;
; 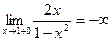 .
.
Прямые х = 1 и (в силу симметрии графика) 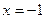 – вертикальные асимптоты.
– вертикальные асимптоты.
4. 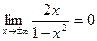 . Прямая у = 0 (ось абсцисс) – двухсторонняя горизонтальная асимптота.
. Прямая у = 0 (ось абсцисс) – двухсторонняя горизонтальная асимптота.
5. 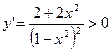 при всех допустимых значениях х. Экстремумов нет, функция возрастает на интервалах
при всех допустимых значениях х. Экстремумов нет, функция возрастает на интервалах 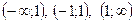 .
.
6. 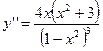 , y" = 0 при х = 0. Знаки второй производной показаны на рис. 8.7.
, y" = 0 при х = 0. Знаки второй производной показаны на рис. 8.7.
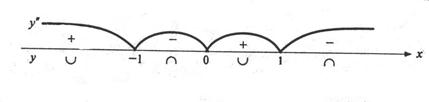
Рис. 8.7
Функция выпукла вниз на интервалах 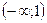 и
и 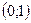 и выпукла вверх на интервалах
и выпукла вверх на интервалах 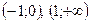 . Хотя ƒ"(х) меняет свой знак при переходе через три точки
. Хотя ƒ"(х) меняет свой знак при переходе через три точки
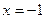 ,
, 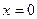 ,
, 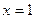 , но график функции имеет только одну точку перегиба х = 1, ибо в двух других точках
, но график функции имеет только одну точку перегиба х = 1, ибо в двух других точках 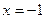 ,
, 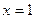 функция не определена.
функция не определена.
7. Точка пересечения графика с осями единственная – начало координат (0;0).
График функции показан на рис. 8.8.
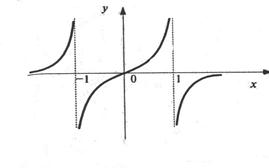
Рис. 8.8
8.95. Исследовать функцию y = (x - 1) ex и построить ее график.
Решение:
1. Область определения 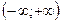 .
.
2. Функция общего вида, так как ƒ (- х) = (- х - 1) 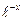
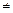
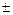 ƒ (х).
ƒ (х).
3. Так как функция определена и непрерывна на всей числовой оси, то вертикальных асимптот нет.
4. 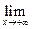 (х - 1) ex = ∞;
(х - 1) ex = ∞; 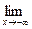 (х - 1) ex = [ ∞∙0] =
(х - 1) ex = [ ∞∙0] = 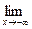
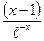 =
= 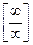 =
= 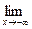
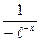 = 0. Следовательно, прямая у = 0 (ось абсцисс) является левосторонней горизонтальной асимптотой.
= 0. Следовательно, прямая у = 0 (ось абсцисс) является левосторонней горизонтальной асимптотой.
5. у ' = ex + (х - 1) ex = х ex. Производная обращается в нуль в точке х = 0. Знаки производной показаны на рис. 8.9.
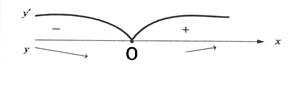
Рис. 8.9
Таким образом, функция убывает на интервале (-∞; 0), возрастает на интервале
(0; +∞); х= 0 – точка минимума и ƒmin (0) = -1.
6. у" = ex + xex = ex (x + 1 ); y" = 0 при х = - 1. Производная y"<0, если х + 1 < 0, т.е. на интервале 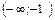 . На интервале
. На интервале 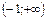 у" > 0. Таким образом, функция выпукла вверх на интервале
у" > 0. Таким образом, функция выпукла вверх на интервале 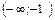 и выпукла вниз на интервале
и выпукла вниз на интервале 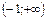 ; х = -1 – точка перегиба.
; х = -1 – точка перегиба.
7. Точка пересечения с осью ординат (0; -1), с осью абсцисс – (1;0). График функции изображен на рис. 8.10.
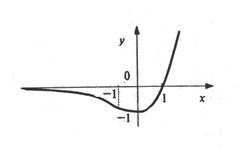
Рис. 8.10
Найти асимптоты графика функции:
8.100. у = 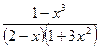 . 8.101. у =
. 8.101. у = 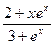 . 8.102. у =
. 8.102. у = 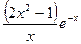 .
.
8.103. у = 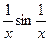 . 8.104. у =
. 8.104. у = 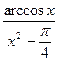 . 8.105. у =
. 8.105. у = 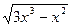 .
.
8.106. у = 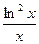 . 8.107. у =
. 8.107. у = 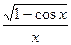 .
.
Исследовать функции и построить их графики:
8.108. у = 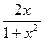 . 8.109. у =
. 8.109. у = 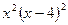 . 8.110. у =
. 8.110. у = 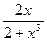 .
.
8.111. у = 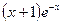 . 8.112. у =
. 8.112. у = 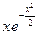 . 8.113. у =
. 8.113. у = 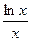 .
.
8.114. у = 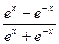 . 8.115. у =
. 8.115. у = 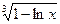 . 8.116. у = e
. 8.116. у = e 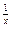 .
.
8.117. у = 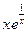 . 8.118. у =
. 8.118. у = 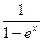 . 8.119. у = sin
. 8.119. у = sin 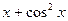 .
.
8.120. у =  . 8.121. у =
. 8.121. у = 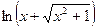 . 8.122. у =
. 8.122. у = 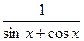 .
.
8.123. у = 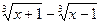 . 8.124. у =
. 8.124. у = 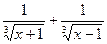 .
.
8.6. Применение производной в задачах с экономическим содержанием
 2015-03-22
2015-03-22 1244
1244
