2015-03-22
6864
а) Приращение функции ∆ у = f (x + ∆ x) – f (x) = f (2 + ∆ x) – f (2) = ((2 + ∆ x)2 + (2 + ∆ x) + 1) – (22 + 2 + 1) = 5∆ x + ∆ x 2. Выделяя линейную относительно ∆ x часть приращения функции, получаем, что dy = 5∆ x = 5 dx.
б) Дифференциал функции dy = (x 2 + x + 1)′ dx = (2x + 1) dx = (2∙2 + 1) dx = 5 dx.
9.2. Найти 1,0050,5; 1,035.
Решение. Получим вначале приближенную формулу для вычисления любой n -й степени. Полагая f (x) = xn, найдем f ′(x) = nxn -1 и в соответствии с (9.6):
(x + ∆ x) n ≈ xn + nxn -1∆ x. В данном примере для x = 1:
1,0050,5 ≈ 1 + 0,5∙0,005 = 1,0025; 1,035 ≈ 1 + 5∙0,03 = 1,15.
9.3. Использую понятие дифференциала, вычислить приближенно arcsin 0,51.
Решение. Рассмотрим функцию y = arcsin x. Полагая x = 0,5, ∆ x = 0,01 и применяя формулу (9.6), имеем:
arcsin(x + ∆ x) ≈ arcsin x + (arcsin x)′ ∆ x = arcsin x + 
.
Следовательно,
arcsin 0,51 ≈ arcsin 0,5 + 
9.4. С какой точностью может быть вычислен объем шара, если его радиус измерен с точностью до 1%?
Решение. Объем шара радиуса x равен f (x) = (4/3) πx 3. Найдем f′ (x) = 4 πx2,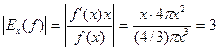 
и по формуле (9.7) 
.
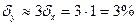9.5. Найти количество лет, в течение которых первоначальная сумма вклада увеличится в два раза, если ставка банковского процента (за год) равна r.
Решение. Найдем количество лет T, в течение которых первоначальная сумма вклада увеличится в два раза. Так как за год вклад увеличивается в (1 + r /100) раз, то за T лет вклад увеличится в (1 + r /100) T раз. Таким образом, необходимо решить уравнение (1 + x /100) T = 2. Логарифмируя, получаем T ln(1 + r /100) = ln2, откуда T = 
.
Для приближенного вычисления значения ln(1 + r /100) используем понятие дифференциала. Получим вначале приближенную формулу для вычислении ln x. Полагая
f (x)= ln x, найдем f′ (x) = 1/ x и в соответствии с (9.6) ln(x + ∆ x) ≈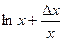 
. В данном примере для x = 1, ∆ x = r /100 получим ln(1 + r /100) = ln1 + r /100 = r /100. Таким образом T ≈ 100 ln(2/ r). Так как ln2 ≈ 0,7, получаем, что время удвоения вклада T ≈ 70/ r (лет).
9.6. Найти dy и d 2 y, если y = 
.
Решение: 
; 
.
Найти приращения функций и их дифференциалы и вычислить их значения при заданных x и ∆ x:
9.7.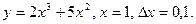 
9.8.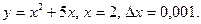 
9.9. 
Найти дифференциалы первого порядка функций и вычислить их значения при заданных x и ∆ x:
9.10. 
9.11. 
9.12.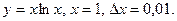 
Найти дифференциалы первого порядка функций:
9.13.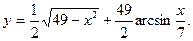 
9.14.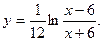 
9.15. 
9.16.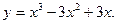 
9.17. 
9.18. 
9.19. 
9.20. 
9.21.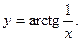 
9.22.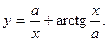 
9.23.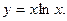 
9.24. 
9.25.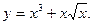 
9.26. 
9.27. 
9.28. 
9.29. 
9.30. 
9.31. 
9.32. 
Найти дифференциалы второго порядка функций:
9.33. 
9.34. 
9.35. 
9.36. 
9.37. 
9.38.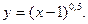 
9.39. 
9.40.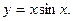 
Используя понятие дифференциала, приближенно вычислить:
9.41. е 0,2. 9.42. ln 1,02. 9.43. 170,25.
9.44. arcsin 0,54. 9.45. 1.021/3. 9.46. cos 151o.
9.47. sin 29o. 9.48. arctg 1,05. 9.49. lg 11.
9.50. Показать, что относительная погрешность в 1% при определении длины радиуса влечет за собой относительную погрешность приблизительно в 2% при вычислении площади круга и поверхности шара.
9.51. Найти время удвоения вклада в банк, если ставка банковского процента за год составляет 5% годовых.
