2015-03-22
710
Пусть функция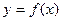 
интегрируема на произвольном отрезке 
.
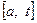Несобственным интегралом (первого рода)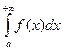 
называется предел функции 
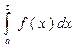при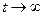 
, т.е.
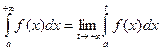(11.22)
Если предел, стоящий в правой части равенства (11.22), существует и кончен то
соответствующий несобственный интеграл называется сходящимся; в противном случае — расходящимся.
Аналогично, по определению,
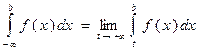, (11.23)
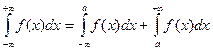, (11.24)
где а — некоторое число. При этом несобственный интеграл, стоящий
в левой части равенства (11.24), называется сходящимся, если сходятся оба несобственных интеграла из правой части этого равенства; в противном случае — расходящимся.
11.73. Вычислить интегралы:
а)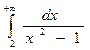 
; б) 
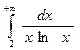; в)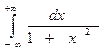 
;
если они сходятся.
Решение. По определению (11.22), получаем
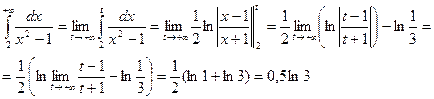
б) по определению,
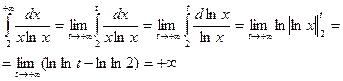
т.е. данный интеграл расходится.
в) Полагая в определении (11.24), что а = 0, учитывая четность подынтегральной функции, имеем
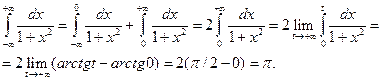
Б. Несобственные интегралы от неограниченных функций
