2015-03-22
1100
Раздел II. Введение в анализ
Глава 5. Функция
Краткая теория
1. Если каждому элементу (значению) 
множества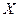 
поставить в соответствие определенный элемент (значение) 
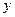множества 
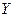, то говорят, что на множестве 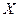задана функция 
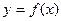; при этом множество 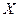называется областью определения функции 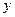, а множество 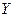- областью значений функции .
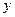2. Функция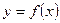 
называется четной, если для любых значений из области определения функции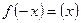 
, и нечетной, если 
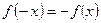. В противном случае 
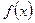- функция общего вида.
3. Функция 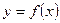называется возрастающей (убывающей) на некотором промежутке 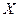, если большему значению аргумента соответствует большее (меньшее) значение функции 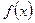. Возрастающие или убывающие функции называются монотонными.
4. Функция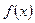 
называется ограниченной на промежутке 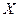, если существует такое число 
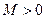, что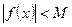 
, для всех 
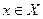. В противном случае функция называется неограниченной.
5. Если функция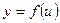 
есть функция переменной 
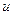(определенной на множестве 
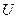с областью значений 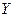), а переменная 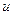, в свою очередь, также является функцией 
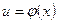(определенной на множестве 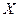с областью значений 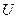), то заданная на множестве 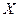функция 
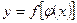называется сложной функцией.
6. Основные элементарные функции:
а) степенная функция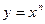 
;
б) показательная функция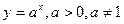 
;
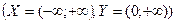в) логарифмическая функция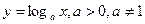 
;
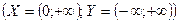г) тригонометрические функции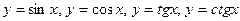 
;
д) обратные тригонометрические функции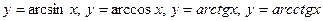 
.
7. Функции, построенные из основных элементарных функций при помощи конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
8. Функция 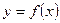называется периодической с периодом 
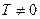, если 
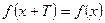для любых .
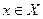а)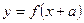 
- сдвигает график 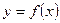параллельно оси 
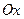на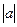 
единиц, (
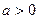- влево, 
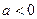- вправо);
б)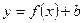 
- сдвигает график 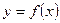параллельно оси 
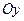на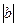 
единиц (
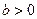- вверх, 
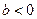- вниз);
в)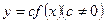 
- растягивает в 
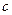раз 
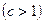или сжимает 
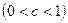график 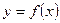относительно ос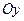и ; при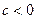 
симметрично отображает график относительно оси ;
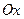г)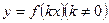 
- растягивает в 
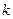раз 
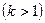или сжимает 
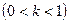график 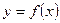относительно ос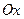и , при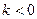 
симметрично отображает график относительно оси .
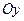10. Абсолютная величина (модуль) действительного числа :
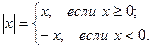
5.1. Найти область определения функции
.
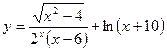Решение. Так как выражение под корнем четной степени должно быть неотрицательно, знаменатель дроби отличен от нуля, а выражение, стоящее под знаком логарифма, должно быть положительно, то область определения функции найдем из системы неравенств:
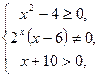или 
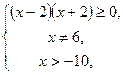откуда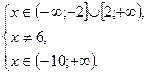 
Значения переменной , которые удовлетворяют всем неравенствам системы одновременно, есть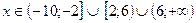 
.
5.2. Найти область значений функции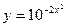 
.
Решение. Воспользуемся определением обратной функции, в соответствии с которым область ее определения будет являться областью значений исходной функции. Найдем функцию, обратную к функции 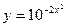, выражая через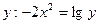 
или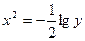 
.
Так как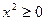 
, то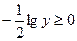 
, откуда 
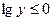и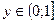 
, т.е. найденный полуинтервал и является областью значения искомой функции.
5.3. Выяснить четность (нечетность) функции:
а)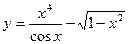 
; б)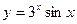 
.
Решение:
а) Найдем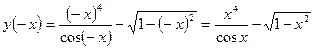 
Так как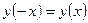 
, то по определению (п.2) искомая функция является четной;
б)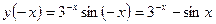 
так как 
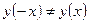и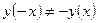 
, то по определению (п. 2) искомая функция является функцией общего вида.
5.4. Найти основной (наименьший) период функции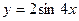 
.
Решение: По определению периодической функции (п. 8)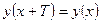 
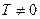для любых и . Для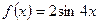 
имеем:
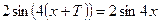, или 
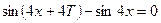, откуда 
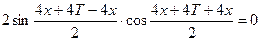. т.е. 
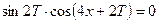. Полученное равенство будет выполняться при любых , т.е. тождественно, если сомножитель, не содержащий , будет равен нулю, т.е. 
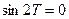и наименьшее (не равное нулю) 
.
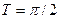5.5. Постоянные издержки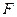 
(не зависящие от числа х произведенной продукции) составляют 125 тыс. руб. в месяц, а переменные издержки 
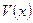(пропорциональные ) – 700 руб. за каждую единицу продукции. Цена единицы продукции 1200 руб. Найти объем продукции , при котором прибыль равна: а) нулю (точка безубыточности); б) 105 тыс. руб. в месяц.
Решение:
а) Издержки производства единиц продукции составят: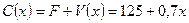 
(тыс. руб.). Совокупный доход (выручка) от реализации этой продукции 
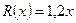, а прибыль 
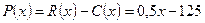(тыс. руб.). Точка безубыточности, в которой 
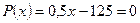, равна 
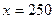(ед.).
б) прибыль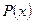 
равна 105 (тыс. руб.), т.е. 
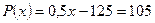при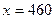 
(ед.).
5.6. Продолжительность выполнения 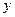(мин.) при повторных операциях связана с числом этих операций зависимостью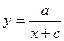 
. Вычислить, сколько минут выполняется работа при 50 операциях, если известно, что при 
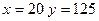, а при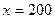 
.
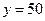Решение. Найдем параметры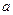 
и 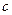, учитывая, что 
, 
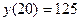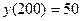. Имеем систему:
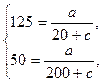
решая которую найдем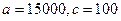 
.
Итак,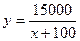 
и при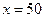 
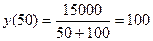(мин.).
Найти области определения функций:
5.12.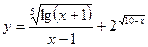 
.
5.13.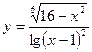 
.
5.14.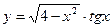 
.
5.15.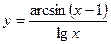 
.
5.16.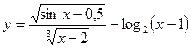 
.
Найти области значений функций:
5.17.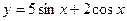 
.
5.18.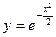 
.
5.19.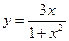 
.
5.20.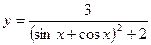 
.
5.21.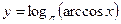 
.
Выяснить четность (нечетность) функций:
5.22.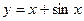 
.
5.23.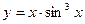 
.
5.24.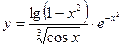 
.
5.25.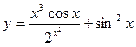 
.
5.26.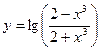 
.
Найти наименьший период функций или доказать их непериодичность:
5.27.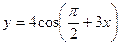 
.
5.28.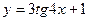 
.
5.29.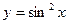 
.
5.30.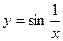 
.
5.31.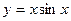 
.
5.32. Дана функция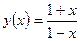 
, найти 
.
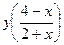5.33. Дана функция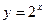 
,найти 
.
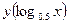5.34. Известно, что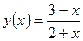 
, а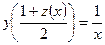 
. Найти 
.
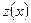5.35. Известно, что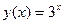 
, а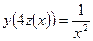 
. Найти .
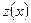5.38. Предприятие купило автомобиль стоимостью 150 тыс. руб. Ежегодная норма амортизации составляет 9 %. Полагая зависимость стоимости автомобиля от времени линейной, найти стоимость автомобиля через 4,5 года.
5.39. Зависимость уровня потребления 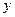некоторого вида товаров от уровня дохода семьи выражается формулой: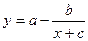 
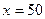
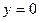. Найти уровень потребления товаров при уровне дохода семьи 158 ден. ед. Известно, что при 
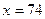
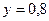; при 
; при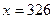 
.
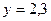5.40. Банк выплачивает ежегодно 5% годовых (сложный процент). Определить: а) размер вклада через 3 года, если первоначальный вклад составил 10 тыс. руб.;
б) размер первоначального вклада, при котором через 4 года вклад (вместе с процентными деньгами) составит 10000 руб.
Указание. Размер вклада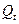 
через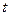 
лет определяется по формуле 
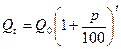, где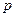 
- процентная ставка за год, 
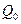- первоначальный вклад.
