1. Пусть функция 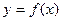 задана на отрезке
задана на отрезке 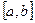 . Разобьем отрезок
. Разобьем отрезок 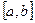 на
на 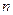 элементарных отрезков точками
элементарных отрезков точками 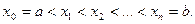
В каждом из отрезков разбиения 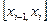 выберем произвольно точку
выберем произвольно точку 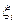 и положим
и положим 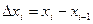 , где
, где 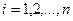 . Тогда сумма вида
. Тогда сумма вида
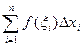 (11.1)
(11.1)
называется интегральной суммой для функции 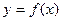 на отрезке
на отрезке 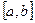 .
.
Пусть существует и конечен предел  интегральной суммы (11.1) при стремлении к нулю длины максимального элементарного отрезка
интегральной суммы (11.1) при стремлении к нулю длины максимального элементарного отрезка 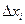 , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка 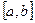 на части и способа выбора точек
на части и способа выбора точек 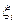 на отрезках разбиения. Тогда функции
на отрезках разбиения. Тогда функции 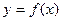 называется интегрируемой на
называется интегрируемой на 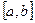 , а число
, а число  - определенным интегралом от
- определенным интегралом от 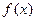 на
на 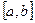 , и обозначается
, и обозначается  :
:
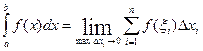 (11.2)
(11.2)
Достаточным условием интегрируемости функции является ее непрерывность на рассматриваемом отрезке.
2. Свойства определенного интеграла:
1) 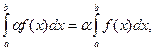 где
где 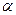 - некоторое число. (11.3)
- некоторое число. (11.3)
2) 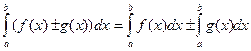 . (11.4)
. (11.4)
3) 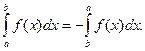 (11.5)
(11.5)
4) 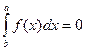 (11.6)
(11.6)
5 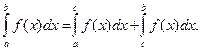 (11.7)
(11.7)
6) Теорема о среднем. Если функция 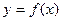 непрерывна на отрезке
непрерывна на отрезке 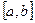 , то найдется такое значение
, то найдется такое значение 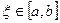 ,что
,что
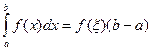 (11.8)
(11.8)
7) Если функция 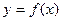 - четная, то
- четная, то
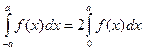 (11.9)
(11.9)
Если функция 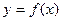 – нечетная, то
– нечетная, то
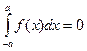 (11.10)
(11.10)
8) Формула Ньютона –Лейбница. Определенный интеграл от непрерывной на отрезке 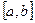 функции
функции 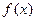 равен приращению любой ее первообразной
равен приращению любой ее первообразной 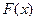 на этом отрезке:
на этом отрезке:
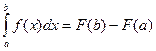 , (11.11)
, (11.11)
или
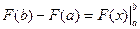
9) Замена переменной в определенном интеграле. Если функция 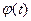 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 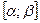 ,
, 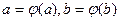 и функция непрерывна в каждом точке
и функция непрерывна в каждом точке 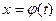 , где
, где 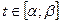 , то
, то
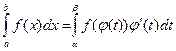 (11.12)
(11.12)
10) Интегрирование по частям определенного интеграла. Если функции 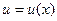 и
и 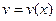 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 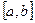 , то
, то
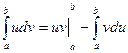 . (11.13)
. (11.13)
11.1. Методы вычисления определенного интеграла
11.1. Вычислить определенные интегралы:
а) 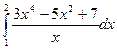 ; б)
; б) 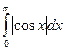 ; в)
; в) 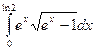 ;
;
г) 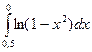 ; д)
; д) 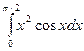 ; е)
; е) 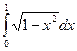 .
.
Решение:
а) используя эквивалентное преобразование подынтегральной функции (почленное деление числителя на знаменатель) и свойства (11.3),(11.4) определенного интеграла, получаем
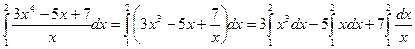 .
.
Все три интеграла – табличные; согласно (11.11), окончательно имеем:
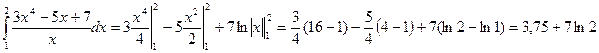 .
.
б) Так как
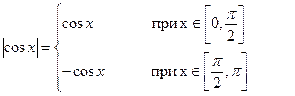
то (см. (11.7))
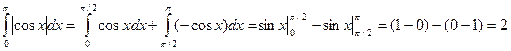
в) Воспользуемся заменой переменной: пусть 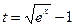 . Тогда
. Тогда 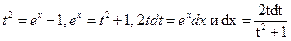 . Найдем пределы интегрирования по переменной t: если
. Найдем пределы интегрирования по переменной t: если 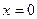 , то
, то 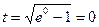 ;если
;если 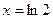 , то
, то 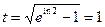 .Искомый интеграл теперь принимает вид:
.Искомый интеграл теперь принимает вид:
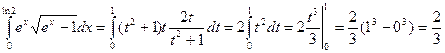 .
.
г) Воспользуемся формулой (11.13) интегрирования по частям: пусть 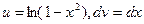 . Тогда
. Тогда 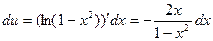 ,
, 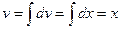 и (см .(10.13))
и (см .(10.13))
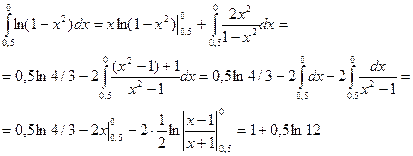
д) Как было отмечено выше (см. § 10.3), данный интеграл находиться с помощью последовательного применения формулы интегрирования по частям. Пусть 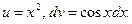 . Тогда
. Тогда 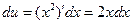 ,
, 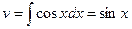 и (см. (11.13)).
и (см. (11.13)).
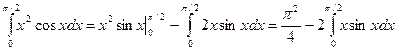 .
.
Для нахождения последнего интеграла вновь применяем формулу (11.13): 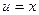 ,
, 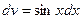 . Тогда
. Тогда 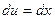 ,
, 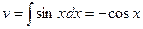 и
и
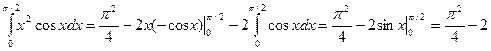 .
.
е) Воспользуемся тригонометрической подстановкой 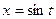 . Будем полагать, что
. Будем полагать, что 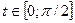 . Если
. Если 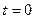 , то
, то 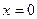 ; если
; если 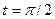 , то
, то 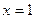 . Тогда
. Тогда 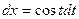 и
и
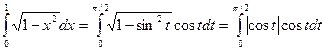 .
.
Так как 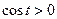 при
при 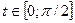 ,
, 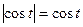 . Применяя тригонометрическую формулу понижения степени, получаем:
. Применяя тригонометрическую формулу понижения степени, получаем:
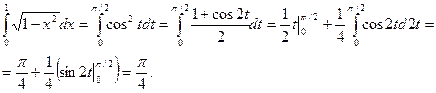
Вычислить определенные интегралы:
11.2. 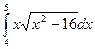 . 11.3.
. 11.3. 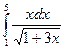 . 11.4.
. 11.4. 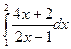 . 11.5.
. 11.5. 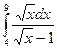 .
.
11.6. 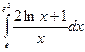 . 11.7.
. 11.7. 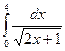 . 11.8.
. 11.8. 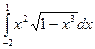 . 11.9.
. 11.9. 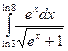 .
.
11.10. 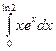 . 11.11.
. 11.11. 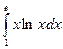 . 11.12.
. 11.12. 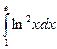 . 11.13.
. 11.13. 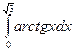 .
.
11.14. 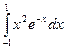 . 11.15.
. 11.15. 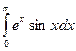 . 11.16.
. 11.16. 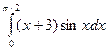 . 11.17.
. 11.17. 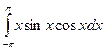 .
.
11.18. 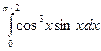 . 11.19.
. 11.19. 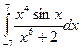 . 11.20.
. 11.20. 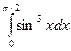 . 11.21.
. 11.21. 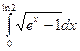 .
.
11.22. 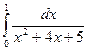 . 11.23.
. 11.23. 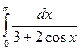 . 11.24.
. 11.24. 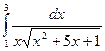 . 11.25.
. 11.25. 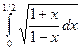 .
.
11.26. 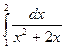 . 11.27.
. 11.27. 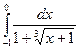 . 11.28.
. 11.28. 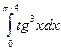 . 11.29.
. 11.29. 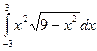 .
.
11.2. Геометрические приложения определенного интеграла.
 2015-03-22
2015-03-22 913
913








