5. Длина  дуги кривой
дуги кривой 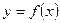 , заключенной между точками с абсциссами
, заключенной между точками с абсциссами
 , определяется по формуле
, определяется по формуле
 (11.18)
(11.18)
Площадь поверхности вращения
6. Площадь поверхности, образованной вращением вокруг оси 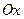 кривой
кривой 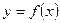 , заключенной между точками с абсциссами
, заключенной между точками с абсциссами  , определяется по формуле
, определяется по формуле
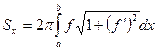 (11.19)
(11.19)
Объемы тел вращения
 7. Если функция
7. Если функция  знакопостоянна на отрезке
знакопостоянна на отрезке  , то объем
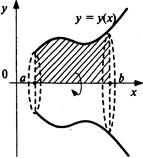
, то объем  тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями
тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 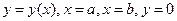 (см. рис. 11.4), вычисляется по формуле
(см. рис. 11.4), вычисляется по формуле
 (11.20)
(11.20)
Рис. 11.4
 Аналогично, объем
Аналогично, объем 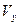 тела, образованного при вращение вокруг оси
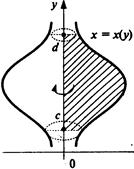
тела, образованного при вращение вокруг оси  плоской фигуры,ограниченной линиями
плоской фигуры,ограниченной линиями  (см.рис. 11.5), вычисляется по формуле
(см.рис. 11.5), вычисляется по формуле
 (11.21)
(11.21)
Рис. 11.5
11.30. Найти площади плоских фигур, ограниченных линиями:
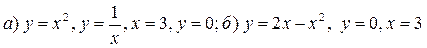
(фигура расположена в первой четверти);
Решение:
 а) Искомая площадь
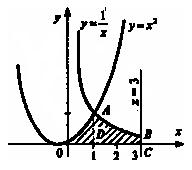
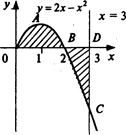
а) Искомая площадь 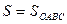 - это площадь под «кривой» ОАВ (см. рис. 11.6) на отрезке [0; 3].
- это площадь под «кривой» ОАВ (см. рис. 11.6) на отрезке [0; 3].
Линия ОАВ состоит из части ОА параболы  ичасти АВ гиперболы
ичасти АВ гиперболы  . Соответственно, площадь
. Соответственно, площадь  найдем как
найдем как
сумму двух площадей:  , каждую из которых Рис.11.6 вычислим, опираясь на геометрический смысл определенного интеграл(см. формулу (11.14)). Решая систему
, каждую из которых Рис.11.6 вычислим, опираясь на геометрический смысл определенного интеграл(см. формулу (11.14)). Решая систему
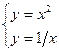
находим координаты точки А: (1, 1).
Тогда  ,
, 
 и
и  (ед.²).
(ед.²).
б) Фигура искомой площади  состоит из двух криволинейных треугольников: AOB и BCD, расположенных (соответственно) выше и ниже оси Ох (см.рис. 11.7). Площадь этих треугольников найдем по формулам (11.14) и (11.15):
состоит из двух криволинейных треугольников: AOB и BCD, расположенных (соответственно) выше и ниже оси Ох (см.рис. 11.7). Площадь этих треугольников найдем по формулам (11.14) и (11.15):
Рис. 11.7

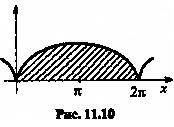 Тогда
Тогда  (eд.²)
(eд.²)
11.31. Найти площадь фигуры, ограниченной осью Ох и циклоидой 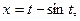
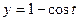 на отрезке [0; 2
на отрезке [0; 2 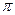 ] (см. рис. 11.10).
] (см. рис. 11.10).
Решение. Используя формулу (11.17), получаем:

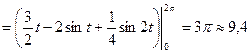 (ед.²).
(ед.²).
11.32. Найти длину дуги полукубической параболы  от начала координат до точки с координатами (4/3,
от начала координат до точки с координатами (4/3,  /9). Решение. Указанный участок кривой расположен в первой четверти и задается уравнением
/9). Решение. Указанный участок кривой расположен в первой четверти и задается уравнением  . Так как в этом случае
. Так как в этом случае 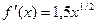 то, применяя формулу (11.18), получаем
то, применяя формулу (11.18), получаем 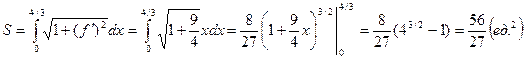
11.33. Найти площадь поверхности, образованной вращением циклоиды  ,
, 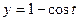 при
при 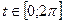 (см. рис. 11.10) вокруг оси Ох.
(см. рис. 11.10) вокруг оси Ох.
Решение. Для получения формулы площади поверхности вращения в случае параметрического задания кривой достаточно произвести соответствующую замену переменной в исходной формуле (11.19).
Более точно, если для кривой 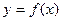 , где
, где  , имеем
, имеем 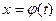 ,
,  ,
,  и
и  , то
, то  .
.
Полагая теперь 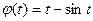 ,
,  , получаем выражения для искомой площади поверхности:
, получаем выражения для искомой площади поверхности:
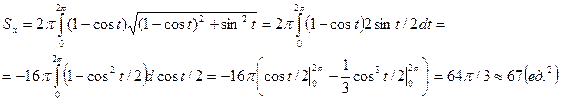
11.35.. Найти объем тела, образованного вращением вокруг оси Ох круга единичного радиуса с центром в точке (0; 2)
Решение. Отметим, что тело указанного вида в геометрии называется тором.
 Искомый объем
Искомый объем 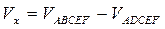 , где
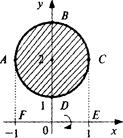
, где  — объемы, полученные при вращении вокруг оси Ох фигур, ограниченных соответственно линиями ABCEF и ADCEF (рис. 11.13). Уравнения полуокружностей ABC и ADC имеют вид:
— объемы, полученные при вращении вокруг оси Ох фигур, ограниченных соответственно линиями ABCEF и ADCEF (рис. 11.13). Уравнения полуокружностей ABC и ADC имеют вид:
 (соответственно).
(соответственно).
Рис. 11.13 Используя (11.20),(11.4), получаем:
 .
.
Применяя (11.9) и результат примера 11.1, е, окончательно имеем
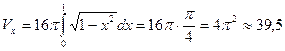 (ед.³)
(ед.³)
Найти площадь фигур, ограниченных линиями:
11.36. 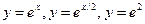 . 11.37.
. 11.37.  .
.
11.38. 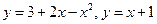 11.39.
11.39.  .
.
11.40.  (фигура расположена в первой четверти).
(фигура расположена в первой четверти).
11.41.  . 11.42.
. 11.42.  .
.
11.43.  . 11.44.
. 11.44.  .
.
11.45.  .
.
11.46.  .
.
11.47.  .
.
11.48.  .
.
11.49. 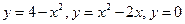 (фигура расположена во второй четверти).
(фигура расположена во второй четверти).
11.50.  .
.
11.51.  и касательная к графику этой функции в точке с абсциссой
и касательная к графику этой функции в точке с абсциссой  .
.
11.52. 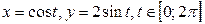 . 11.53.
. 11.53.  .
.
Найти длину дуг следующих кривых:
11.54.  . 11.55.
. 11.55. 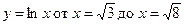 .
.
11.56. 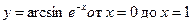
11.57. 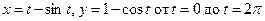 .
.
Найти площадь поверхности вращения, полученных при вращение вокруг оси Ох следующих кривых:
11.58.  . 11.59.
. 11.59.  .
.
11.60. 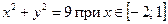 . 11.61.
. 11.61.  .
.
Найти объем тел, образованных при вращение вокруг оси Ох и Оу плоских фигур, ограниченных линиями:
11.62.  .
.
11.63. 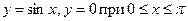 .
.
11.64. 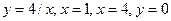 .
.
11.65.  .
.
11.66. 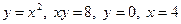 .
.
11.67. 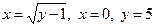 .
.
11.68.  .
.
11.69.  .
.
11.70. 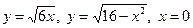 .
.
11.71. 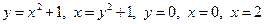 .
.
11.72. Найти объем тела, полученного при вращение фигуры, ограниченной линиями 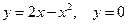 вокруг прямых: а)
вокруг прямых: а) 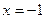 ; б)
; б) 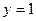 .
.
11.3. Несобственные интегралы
А. Несобственные интегралы с бесконечными пределами интегрирования
 2015-03-22
2015-03-22 3248
3248
