1. Функция 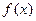 называется непрерывной в точке x0, если она удовлетворяет следующим условиям: 1) определена в точке x0; 2) имеет конечный предел при х → x0 ;
называется непрерывной в точке x0, если она удовлетворяет следующим условиям: 1) определена в точке x0; 2) имеет конечный предел при х → x0 ;
3) этот предел равен значению функции в этой точке: 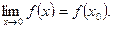 (6.1)
(6.1)
(первое определение).
2. Функция 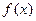 называется непрерывной в точке x0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
называется непрерывной в точке x0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 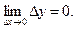 (6.2)
(6.2)
(второе определение).
3. Если функции 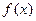 и
и 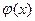 непрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.
непрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.
4. Если функция у = 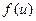 непрерывна в точке u0 =
непрерывна в точке u0 = 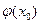 , а функция u=
, а функция u= 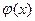 непрерывна в точке x0, то сложная функция у =
непрерывна в точке x0, то сложная функция у = 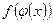 непрерывна в точке x0.
непрерывна в точке x0.
5. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны во всех точках, где они определены.
6. Если не выполнено определение непрерывности (6.1) или (6.2), то функция в точке x0 терпит разрыв, причем:
а) если хотя бы один из односторонних пределов 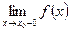 или
или 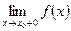
бесконечен, то x0 - точка разрыва второго рода;
б) если оба односторонних предела 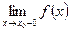 и
и 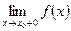 конечны, но не равны между собой, то x0 — точка неустранимого разрыва первого рода;
конечны, но не равны между собой, то x0 — точка неустранимого разрыва первого рода;
в) если оба односторонних предела 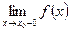 и
и 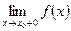 конечны, равны между собой, но не равны
конечны, равны между собой, но не равны 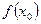 , то x0 — точка устранимого разрыва первого рода.
, то x0 — точка устранимого разрыва первого рода.
6.168. Исследовать на непрерывность функции у = 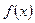 в точке х = 1. В случае разрыва установить его характер в точке х = 1:
в точке х = 1. В случае разрыва установить его характер в точке х = 1:
а) 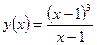 ; б)
; б) 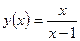 ; в)
; в) 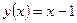 ; г)
; г) 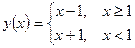 .
.
Решение: а) При х = 1 функция не определена, следовательно, функция в точке
х = 1 терпит разрыв (рис. 6.1): 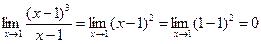 , т.е. конечный предел существует; следовательно, х = 1 — точка устранимого разрыва первого рода. (Доопределив функцию в точке х = 1, т.е. положив
, т.е. конечный предел существует; следовательно, х = 1 — точка устранимого разрыва первого рода. (Доопределив функцию в точке х = 1, т.е. положив 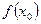 = 0, получим, что новая функция
= 0, получим, что новая функция
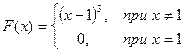 будет уже непрерывна в точке х = 1.)
будет уже непрерывна в точке х = 1.)
6) При x = 1 функция не определена, следовательно, функция в точке x = 1 терпит разрыв (рис. 6.2): 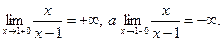
Так как односторонние пределы (достаточно было бы одного) бесконечны, то х = 1 – точка разрыва функции второго рода.
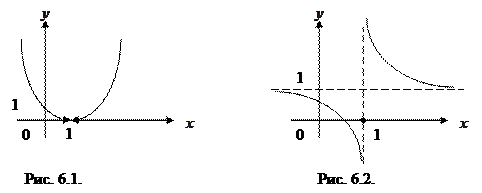 |
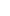
в) При х = 1 функция определена, 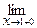 (x -1) = 0,
(x -1) = 0, 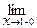 (x -1) = 0, у (1) = 1 - 1 = 0, т.е.
(x -1) = 0, у (1) = 1 - 1 = 0, т.е. 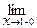 у (х)=
у (х)= 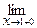 у (х) = у (1) = 0, следовательно, функция в точке х = 1 непрерывна
у (х) = у (1) = 0, следовательно, функция в точке х = 1 непрерывна
(рис. 6.3).
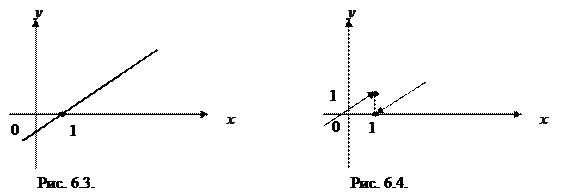 |
г) При х = 1 функция определена, у (1)=0,
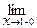 у(х)=
у(х)=  (х +1)=2,
(х +1)=2,  у (х)=
у (х)= 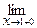 (х -1)=0,
(х -1)=0,
 имеем
имеем 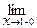 у (х) ≠
у (х) ≠ 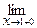 у (х), таким образом, в точке х = 1 функция терпит неустранимый разрыв первого рода (рис. 6.4.)
у (х), таким образом, в точке х = 1 функция терпит неустранимый разрыв первого рода (рис. 6.4.)
 2015-03-22
2015-03-22 772
772








