I. Дифференцирование явных функций
Правила дифференцирования:
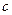 – постоянная,
– постоянная, 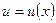 ,
, 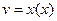 – дифференцируемые функции:
– дифференцируемые функции:
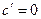 (7.2)
(7.2) 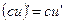 (7.6)
(7.6)
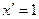 (7.3)
(7.3) 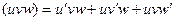 (7.7)
(7.7)
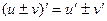 (7.4)
(7.4) 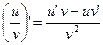 ,
, 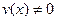 (7.8)
(7.8)
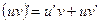 (7.5)
(7.5) 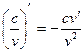 ,
, 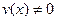 (7.9)
(7.9)
Производная сложной функции. Если 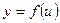 ,
, 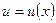 , т.е.
, т.е. 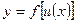 , где
, где 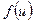 и
и 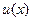 имеют производные, то
имеют производные, то
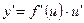 (7.10)
(7.10)
Производная обратной функции. Если 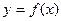 – дифференцируемая и строго монотонная функция на промежутке
– дифференцируемая и строго монотонная функция на промежутке 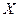 , то функция обратная к данной
, то функция обратная к данной 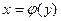 , также дифференцируема и ее производная определяется соотношением:
, также дифференцируема и ее производная определяется соотношением:
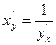 ,
, 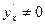 . (7.11)
. (7.11)
Логарифмическая производная. Логарифмической производной функции 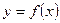 называется производная от логарифма этой функции, т.е.
называется производная от логарифма этой функции, т.е.
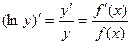 . (7.12)
. (7.12)
Формулы дифференцирования основных элементарных функций:
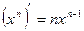 (7.13)
(7.13) 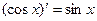 (7.20)
(7.20)
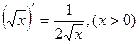 (7.14)
(7.14) 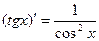 (7.21)
(7.21)
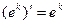 (7.15)
(7.15) 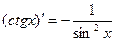 (7.22)
(7.22)
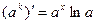 (7.16)
(7.16) 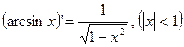 (7.23)
(7.23)
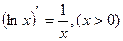 (7.17)
(7.17) 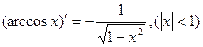 (7.24)
(7.24)
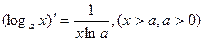 (7.18)
(7.18) 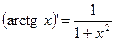 (7.25)
(7.25)
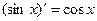 (7.19)
(7.19) 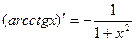 (7.26)
(7.26)
 2015-03-22
2015-03-22 638
638








