Депозит с простой процентной ставкой.
Рассмотрим ситуацию, когда за счёт имущества фонда заключён депозитный договор с кредитной организацией.
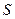 - сумма («тело») депозита
- сумма («тело») депозита
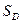 - конечная сумма, включающая в себя «тело» депозита и накопленный процентный доход
- конечная сумма, включающая в себя «тело» депозита и накопленный процентный доход
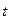 - срок размещения депозита в календарных днях
- срок размещения депозита в календарных днях
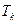 - количество календарных дней в году
- количество календарных дней в году
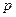 - простая процентная ставка
- простая процентная ставка
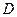 - доход от депозита по состоянию на последний день его размещения
- доход от депозита по состоянию на последний день его размещения
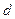 - доход на один календарный день
- доход на один календарный день
Переменные 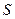 ,
, 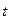 ,
, 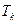 ,
, 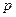 являются существенными условиями депозитного договора, поэтому они всегда известны.
являются существенными условиями депозитного договора, поэтому они всегда известны.
Доход от такого депозита определяется следующим математическим соотношением:
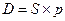
В случае, если необходимо определить доход от депозита, приходящийся на один календарный день года, математическое соотношение принимает следующий вид:
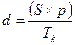 ,
,
При условии, если срок депозита составляет менее одного года (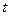 ), и необходимо рассчитать доход от депозита по состоянию на последний день его размещения (
), и необходимо рассчитать доход от депозита по состоянию на последний день его размещения (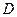 ), соотношение выглядит следующим образом:
), соотношение выглядит следующим образом:
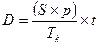
Для определения конечной суммы, подлежащей возврату и включающую в себя «тело» депозита и процентный доход 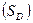 при условии однократного начисления процентов, используется следующее выражение:
при условии однократного начисления процентов, используется следующее выражение:
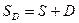
В том случае, когда депозит размещён на несколько лет и проценты начисляются ежегодно, но не выплачиваются, то конечная сумма 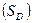 рассчитывается так:
рассчитывается так:
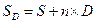 , или
, или 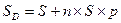
где 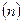 - количество периодов начисления процентов за весь срок размещения депозита.
- количество периодов начисления процентов за весь срок размещения депозита.
В том случае, когда депозит размещён на один год и проценты начисляются ежемесячно, но не выплачиваются, то конечная сумма 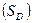 рассчитывается так:
рассчитывается так:
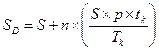 , где
, где
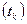 - количество календарных дней периоде, за который банк начисляет проценты (в нашем случае – месяц), а
- количество календарных дней периоде, за который банк начисляет проценты (в нашем случае – месяц), а 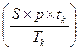 - доход от депозита в расчёте на один календарный месяц.
- доход от депозита в расчёте на один календарный месяц.
Депозит со сложной процентной ставкой.
Для расчёта конечной суммы 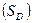 по депозиту со сложным процентом необходимо использовать следующее математическое соотношение:
по депозиту со сложным процентом необходимо использовать следующее математическое соотношение:
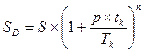
2. Оценка процентных соотношений при расчёте структуры активов и изменения СЧА
Рассмотрим ситуацию, когда необходимо принять решение о возможности размещения депозита за счёт средств фонда. Положим, что:
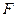 – стоимость активов фонда
– стоимость активов фонда
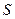 – сумма депозита
– сумма депозита
При этом, согласно Положению о структуре активов, 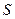 должна составлять не более 25% от
должна составлять не более 25% от 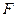 (в случае, если размещаемый депозит является единственным в данной кредитной организации).
(в случае, если размещаемый депозит является единственным в данной кредитной организации).
Для этого воспользуемся следующим соотношением:
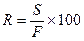 ,
,
где 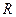 – процентное соотношение суммы депозита к стоимости активов фонда.
– процентное соотношение суммы депозита к стоимости активов фонда.
Если в данной кредитной организации уже размещены депозиты на сумму 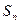 , то возникает необходимость для расчёта коффициента
, то возникает необходимость для расчёта коффициента 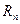 , где
, где 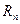 - величина, отражающая процентное соотношение между суммарной стоимостью всех размещённых и вновь размещаемого депозитов в одной кредитной организации и стоимостью активов фонда
- величина, отражающая процентное соотношение между суммарной стоимостью всех размещённых и вновь размещаемого депозитов в одной кредитной организации и стоимостью активов фонда 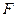 :
:
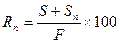
Равно, как 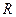 , так и коэффициент
, так и коэффициент 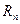 не должен превышать величину, равную 25% стоимости активов фонда.
не должен превышать величину, равную 25% стоимости активов фонда.
Аналогичным образом следует проводить расчёт структуры активов, в случае, когда необходимо принять решение о возможности включения в состав имущества фонда объекта инвестирования. Необходимо учитывать, что для различных объектов инвестирования требования, предъявляемые Положением о составе и структуре активов к коэффициентам 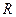 или
или 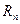 могут отличаться.
могут отличаться.
Рассмотрим ситуацию, когда необходимо оценить величину изменения СЧА в процентах.
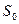 - начальная СЧА
- начальная СЧА
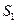 - конечная СЧА
- конечная СЧА
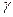 - изменение СЧА
- изменение СЧА
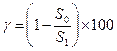
При этом, если 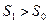 , то коэффициент
, то коэффициент 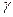 лежит в области положительных значений, если же
лежит в области положительных значений, если же 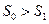 , то коэффициент
, то коэффициент 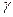 лежит в области отрицательных значений.
лежит в области отрицательных значений.
 2015-03-22
2015-03-22 559
559








