Тема 2.1. Дифференцирование функций

Умения и знания, которые должны приобрести студенты: дифференцировать элементарные функции; составлять уравнение касательной и нормали к кривой; находить производную сложной функции; находить дифференциал функции; находить производные высших порядков.

Повторение теоретических основ:

1. Производная функции (определение).

2. Механический смысл производной.

3. Общее правило нахождения производной.

4. Правила дифференцирования суммы, произведения, частного двух функций: ; ; ;().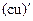

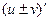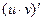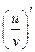5. Таблица производных основных элементарных функций.

6. Сложная функция (определение).

7. Правило дифференцирования сложной функции.

8. Примечания к правилу дифференцирования функций.

Самостоятельная работа № 2,3.

Решение задач на нахождение производных элементарных функций.

Решение задач на нахождение производных сложных функций.

1. Найдите производную функции 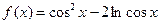, вычислите .

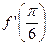2. Найдите вторую производную функции 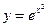, вычислите .

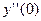3. Найдите производную функции 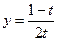, вычислите .

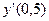4. Найдите производную 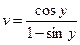, вычислите .

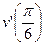5. Найдите производную функции 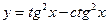, вычислите .

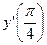6. Найдите вторую производную функции 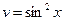и вычислите .

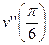7. Найдите производную функции 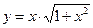, вычислите .

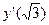8. Найдите производную функции 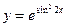, вычислите .

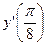9. Найдите производную функции 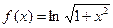, вычислите .

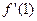10. Найдите производную функции 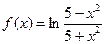, вычислите .

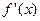Тема 2.2. Приложение производной к исследованию функции и построению графика. Нахождение набольшего и наименьшего значений функции.

Умение и навыки, которые должны приобрести студенты: исследовать функцию по первой и второй производной и строить графики функции по результатам исследования; находить максимальную скорость тела; находить наибольшее и наименьшее значения функции на промежутке.

Повторение теоретических основ:

1. Теорема о признаке возрастания, убывание функции на промежутке.

2. Правило исследования функции на монотонность.

3. Точки экстремума функции: точки максимума и точки минимума.

4. Необходимое условие существования экстремума функции.

5. Достаточное условие существования экстремума функции.

6. Правило исследования функции на экстремум.

7. Выпуклость и вогнутость кривой на промежутке.

8. Теорема о признаке выпуклости и вогнутости кривой на промежутке.

9. Точка перегиба графика функции.

10. Необходимое и достаточное условия существования точки перегиба.

11. Правило исследования функции на выпуклость вогнутость кривой и нахождения точек перегиба графика функции.

12. Упрощенная схема исследования функции для построения графика функции.

13. Физический смысл производной.

14. Алгоритм нахождения наибольшей скорости тела.

15. Правило нахождения наибольшего и наименьшего значений функции на промежутке [a;b].

Самостоятельная работа № 4,5.

Решение задач на исследование функций с помощью производной.

Решение задач на физический и геометрический смысл производной

1. Составьте уравнение касательной к кривой 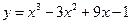в точке .

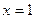2. Тело движется прямолинейно по закону 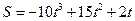. Найдите максимальную скорость движения тела.

3. Исследуйте функцию и постройте ее график: .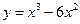

4. Найдите дифференциал функции .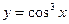

5. Тело движется прямолинейно по закону 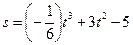. Найдите скорость движения тела в тот момент, когда ускорение равно 0.

6. Найдите наибольшее и наименьшее значение функции 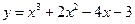на отрезке от -3 до 0.

7. Найдите экстремум функции .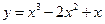

8. Исследуйте функцию и постройте ее график: .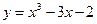

9. Пусть 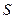путь в метрах, пройденный телом за 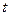секунд при прямолинейном движении, определяется уравнением 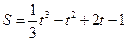. Найдите скорость и ускорение в конце третьей секунды.

10. Определить размеры открытого бассейна объемом 256 куб. м., имеющего квадратное дно, так чтобы на облицовку его стен и дна было израсходовано наименьшее количество материала.