Контрольные задания 1 - 2

Вариант 2

1. Зависимость радиус – вектора частицы от времени дается законом 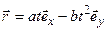, где a и b – положительные постоянные. Найти уравнение траектории в виде зависимости y(x).

2. Однородный цилиндр радиусом R = 0,2 м и массой m = 5 кг вращается вокруг своей оси. Зависимость угловой скорости w вращения цилиндра от времени t дается уравнением w = A + Bt, где В = 8 рад/с². Найти касательную силу F, приложенную к боковой поверхности цилиндра перпендикулярно его оси.

3. В лодке массой М = 240 кг стоит человек массой m = 60 кг. Лодка плывет со скоростью 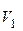= 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью 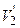= 4 м/с относительно лодки. Найти скорость U движения лодки после прыжка человека, если прыжок совершен в сторону, противоположную движению лодки.

4. Частица массой m = 5 г гармонически колеблется с частотой n = 5 Гц и амплитудой А = 3 см. Найти модуль скорости v частицы в момент времени, когда ее смещение x = 1,5 см.

5. Пусть h₀ – отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а h – соответствующее отношение на высоте h = 3000 м. Найти отношение h/h₀ при Т = 280 К, полагая, что температура и ускорение свободного падения не зависят от высоты.