Итерационная формула Гаусса-Зейделя

Каждая итерация метода Гаусса-Зейделя для задачи (1), (2) состоит из двух шагов и имеет вид

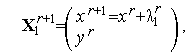(3)

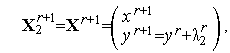(4)

где величины 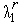, 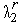– определяются из условий

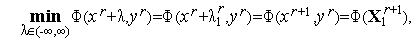(5)

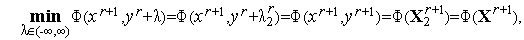(6)

Найдем явное решение задачи (5). Из (5) имеем

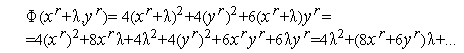(7)

Функция (7) относительно 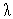является квадратичной функций с положительным коэффициентом при 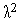и достигает минимума в точке, удовлетворяющей условию

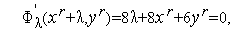
из которого имеем

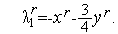(8)

Аналогично явное решение задачи (6) равно

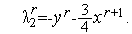(9)

Таким образом, из (3), (4), (8), (9) имеем искомую итерационную формулу метода Гаусса-Зейделя для задачи (1), (2)

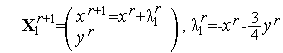(10)

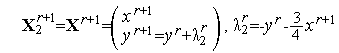(11)

Первая итерация ( 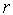=1).

Из формул (10) имеем 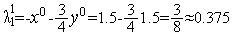и 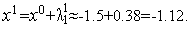Аналогично из формул (11) имеем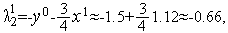 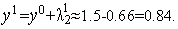Таким образом, 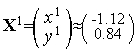(см. рис. 1).

Вторая итерация (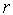 =2).

Аналогично первой итерации, имеем

,

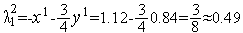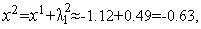
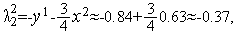
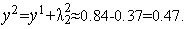
Таким образом, 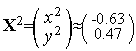(см. рис. 1).

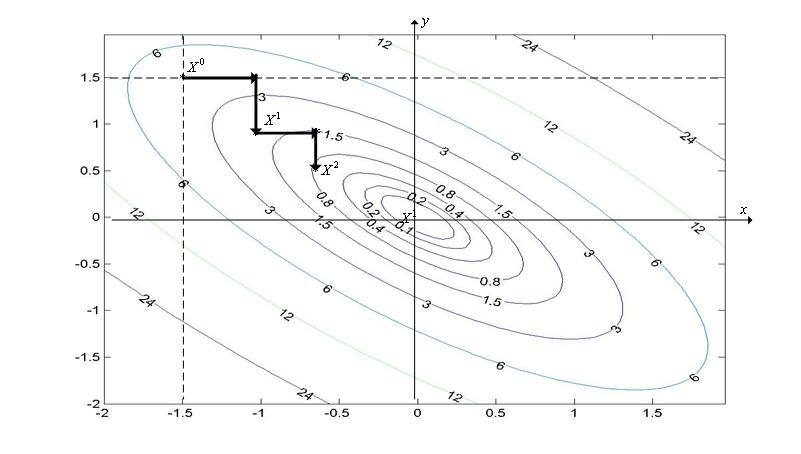Рис. 1. Фрагмент (две итерации) траектории поиска минимума функции (2) методом Гаусса-Зейделя, исходя из точки X ⁰=(x ⁰, y ⁰)=(-1.5,1.5).

6.2 Метод Хука-Дживса

Рассмотрим следующую многомерную задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в -мерном евклидовом пространстве ,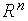

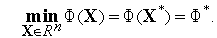(1)

При решении задачи (1) методом Хука-Дживса (методом конфигураций, методом пробных шагов) используются итерационные формулы, аналогичные формулам, используемым в методе Гаусса-Зейделя

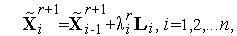(2)

где принято 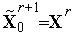, , 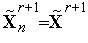вектор 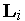определяет направление вдоль 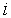-й координатной оси и представляет собой -мерный вектор с компонентами

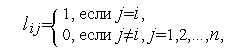
величины 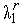, ,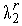..., 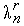– определяются из условий

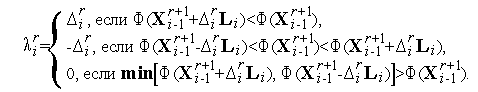(3)

После завершения шагов выполняется спуск в направлении вектора (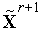 - 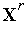) по формуле

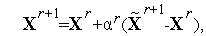(4)

где 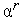- ускоряющий множитель. В различных модификациях метода Хука-Дживса множитель 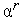может

• приниматься постоянным (обычно, равным 2),
• выбираться из условия ()< (),
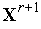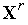• находиться из условия локального минимума функции () при движении из точки 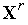в направлении вектора :

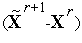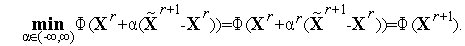(5)

Заметим, что задачи (5) даже в случае одноэкстремальной функции 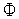() могут быть многоэкстремальными задачами оптимизации и могут быть решены рассмотренными в главе 4 методами решения задач одномерной оптимизации.

Итерации заканчиваются при выполнении одного из стандартных условий окончания итераций:

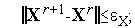(6)

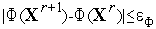
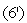
Вектор 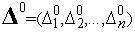является вектором свободных параметров метода - вектором «пробных шагов» по всем координатным осям.

Известна модификация метода Хука-Дживса, в которой точка 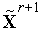определяется не процедурами (2), (3), а методом Гаусса-Зейделя.

Схема метода Хука-Дживса:

1. Задаем начальную точку 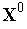, вектор «пробных» шагов 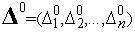и полагаем =0.

2. Последовательно для 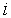=1,2,... по формулам (2), (3) находим точки .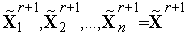

3. Если 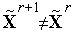, то переходим к п. 4). Иначе уменьшаем длины «пробных» шагов 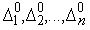, например, вдвое и переходим к п.2).

4. Если условие окончания поиска (6) или (6') выполнено, то полагаем 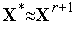и заканчиваем вычисления. Иначе выполняем спуск в направлении вектора 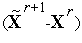по формуле (4), в которой ускоряющий множитель находится, например, из условия (5). Полагаем 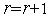и переходим к п. 2

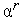Метод Хука-Дживса иллюстрирует рис. 1, на котором показаны линии уровня функции Химмельблау ( =2). Ускоряющий множитель находиться из условия локального минимума функции () при движении из точки 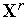в направлении вектора .

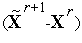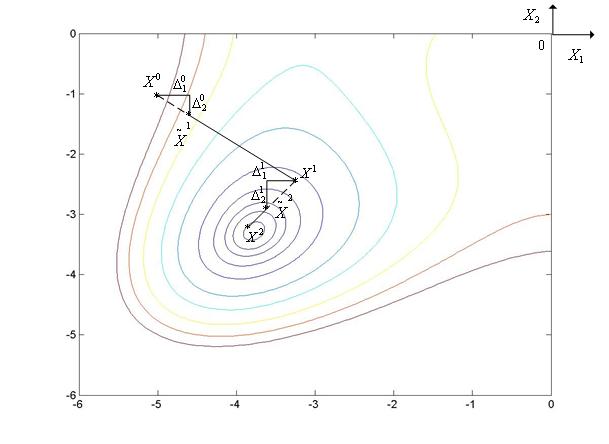Рис. 1. Траектория поиска минимума не овражной функции Химмельблау методом Хука-Дживса.

Метод Хука-Дживса имеет высокую эффективность в случае, если функция () имеет прямолинейный овраг (не обязательно ориентированный вдоль одного из координатных направлений, как в методе Гаусса-Зейделя). При минимизации "овражных" функций, имеющих не прямолинейный овраг, процесс поиска может сильно замедлиться и закончиться далеко от точки истинного минимума (см. рис. 2). На рисунке показаны линии уровня функции Розенброка ( =2).

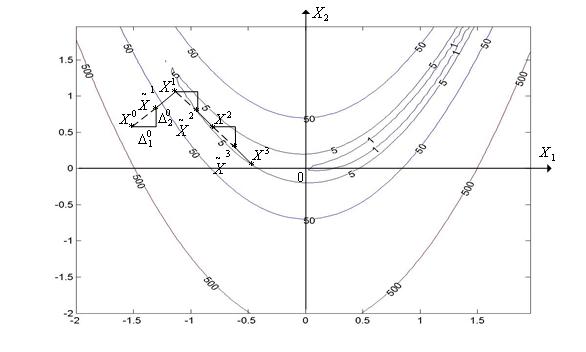Рис. 2. Траектория поиска минимума овражной функции Розенброка методом Хука-Дживса. Ускоряющий множитель α ^r принят равным двум.

6.3 Метод Розенброка

Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в -мерном евклидовом пространстве ,

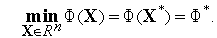(1)

Ортогонализация Грамма-Шмидта.

При решении задачи (1) методом Розенброка (методом вращающихся координат) используется преобразование на каждой итерации системы координат таким образом, чтобы в новой системе координат одна из осей совпадала с направлением предыдущего шага. Остальные оси новой системы координат обычно находят с помощью процедуры ортогонализации Грамма-Шмидта.

Рассмотрим произвольный набор векторов 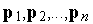пространства 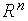. Поставим задачу построить на основе этих векторов ортонормированный набор векторов 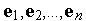того же пространства .

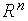Напомним, что набор векторов 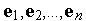называется ортонормированным, если для любых двух векторов из этого набора выполняется условие

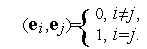(2)

Или, другими словами, набор векторов 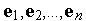ортонормирован, если эти векторы линейно независимы и скалярное произведение любых двух из них равно единице.

Для построения векторов 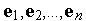применим индуктивный подход. Положим, что

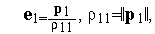(3)

где 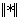- символ евклидовой нормы. Полагая векторы 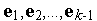уже построенными будем искать вектор 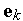в виде

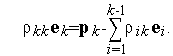(4)

Для отыскания неизвестных множителей 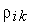умножим (4) скалярно на вектор :

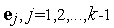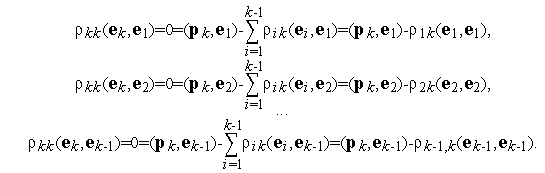
Поскольку 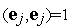, имеем

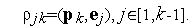(5)

Множитель 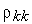найдем из условия :

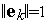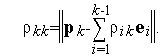(6)

Определение 1. Процесс перехода от векторов 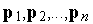к векторам 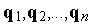согласно формулам (3) – (6) называется ортогонализацией Грамма-Шмидта

Схема метода Розенброка.

Каждая итерация метода Розенброка состоит из двух этапов. В зависимости от модификации метода первый этап может выполняться с использованием различных методов. Рассмотрим применение на первом этапе итерационной формулы метода Гаусса-Зейделя. Приведем формулировку этой формулы, несколько отличную от формулировки, рассмотренной в параграфе 6.1.

Положим 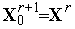, 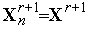и пусть 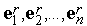- орты системы координат, используемой на -ой итерации. Тогда итерационную формулу метода Гаусса-Зейделя можно записать в виде

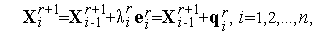(7)

где коэффициенты 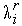находятся из условий

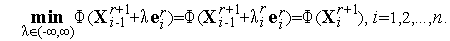(8)

На втором этапе каждой из итераций система векторов 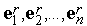с использованием ортогонализации Грамма-Шмидта заменяется новой системой линейно независимых векторов .

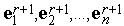Схема метода Розенброка:

1. Задаем начальную точку 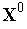, полагаем 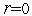, , и орты исходной системы координат обозначаем .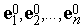

2. Исходя из точки 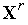по формулам (7), (8) выполняем одну итерацию по методу Гаусса-Зейделя – получаем точку 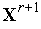и совокупность векторов , ,..., .

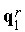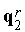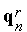3. Если одно из стандартных условий окончания итераций

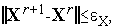(9)

4.

выполнено, то полагаем 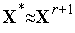, и заканчиваем вычисления. Иначе переходим к п.4).

5. На основе векторов 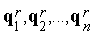находим векторы :

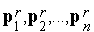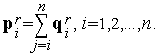(10)

6.

7. С помощью процедуры ортогонализации Грамма-Шмидта (3) –(6) выполняем переход от системы векторов 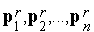к системе векторов 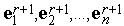, полагаем = +1 и переходим к п. 2

Заметим, что из формулы (10) следует равенство .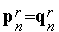

По сравнению с методом Гаусса-Зейделя и методом Хука-Дживса метод Розенброка имеет, как правило, более высокую эффективность на овражных функциях с не прямолинейным оврагом.

Метод Розенброка иллюстрирует рис. 1, на котором показаны линии уровня функции Химмельблау ( =2),

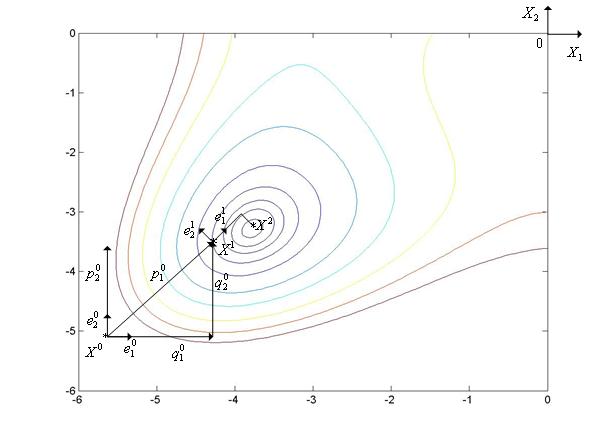Рис. 1. Траектория поиска минимума функции Химмельблау методом Розенброка.

6.4 Метод сопряженных направлений

Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в -мерном евклидовом пространстве ,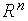

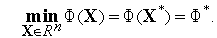(1)

Введем прежде следующие понятия: векторы 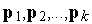, принадлежащие пространству 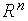, называются векторами сопряженными относительно матрицы A 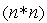(A – ортогональными векторами), если 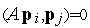для всех .

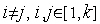В методе сопряженных направлений применяется итерационная формула метода Гаусса-Зейделя в виде, близком к использованному в параграфе 6.3.

Положим 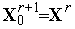и пусть 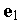, ,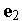..., 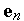- орты используемой системы координат. Тогда итерационную формулу метода Гаусса-Зейделя можно записать в виде

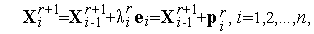(2)

где коэффициенты 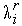находятся из условий

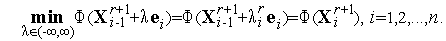(3)

Схема метода сопряженных направлений:

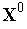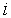1. Задаем начальную точку и полагаем =0, =1.

2. Последовательно для 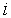=1,2,..., по формулам (2), (3) находим точки , , .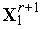

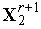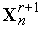3. Исходя из точки 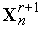, еще раз находим минимум функции () вдоль первого координатного направления - вычисляем координаты точки

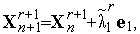(4)

4.
где коэффициент 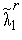находится из условия

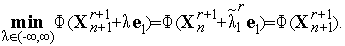(5)

5.

6. Исходя из точки 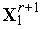, находим минимум функции 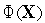вдоль вектора 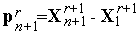- вычисляем

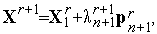(6)

7.
где коэффициент 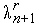находится из условия

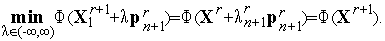(7)

8.

9. Если одно из стандартных условий окончания итераций

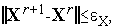(8)

10.

выполнено, то полагаем 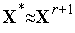, и заканчиваем вычисления. Иначе - полагаем = +1 и переходим к п.2)

Метод сопряженных направлений иллюстрирует рис. 1, на котором показаны линии уровня функции Химмельблау ( =2).

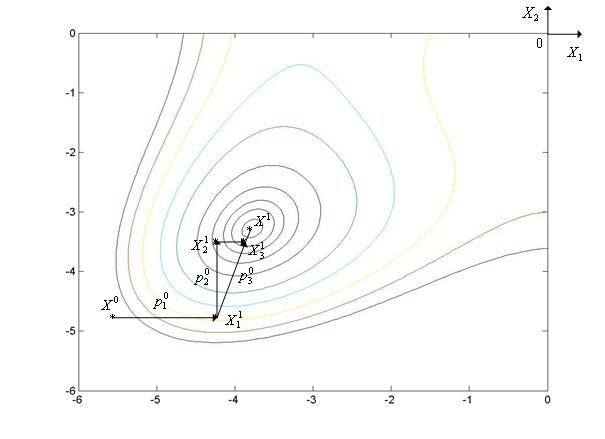Рис. 1. Траектория поиска минимума функции Химмельблау методом сопряженных направлений.

Рассмотрим еще один пример – см. рис. 2, на котором показаны линии уровня двумерной квадратичной функции

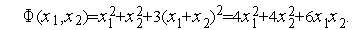(9)

Линии уровня получены с помощью MATLAB-программы, приведенной в параграфе 6.1.

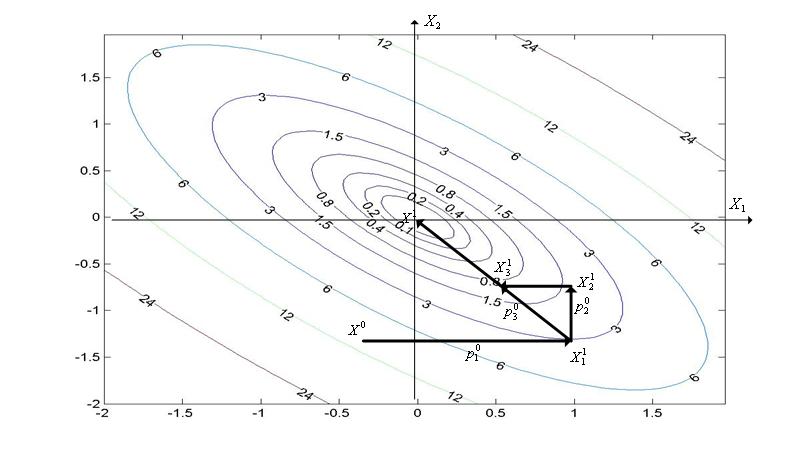Рис. 2. Траектория поиска минимума квадратичной функции (9) методом сопряженных направлений.

Произвольную -мерную квадратичную функцию можно записать в виде

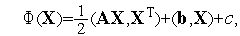(10)

где 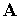– квадратная * матрица, 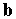– *1 столбец, 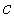– скалярная константа. Например, если положить

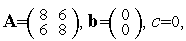то имеем функцию (9):

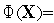
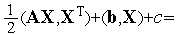
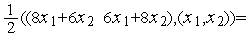
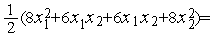
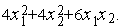
Утверждение 1. В случае минимизации двумерной квадратичной функции (10) методом сопряженных направлений, направления 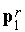, 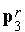являются 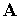-ортогональными.

Доказательство (см. рис. 2). По определению 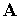-ортогональности для доказательства утверждения достаточно показать, что скалярное произведение

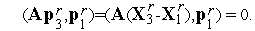(11)

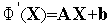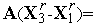
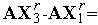
Легко видеть, что производная функции (10) равна . Поэтому 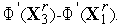Подставляя этот результат в выражение (11), получим .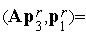

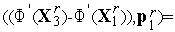
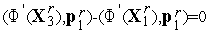Последнее равенство следует из ортогональности пар векторов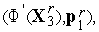

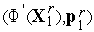
Утверждение 1 объясняет название рассмотренного метода.

Заметим, что при минимизации квадратичной функции методом сопряженных направлений минимум достигается за одну итерацию.

6.5 Симплекс-метод

Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в -мерном евклидовом пространстве ,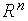

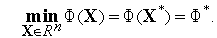(1)

Регулярный симплекс и некоторые операции над ним.

Регулярным симплексом в пространстве 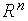называется правильный многогранник, образованный 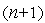-ой равноотстоящими друг от друга вершинами. Для случая 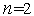– это равносторонний треугольник, для случая 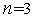– тетраэдр.

Если в пространстве 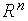необходимо построить регулярный симплекс, одна из вершин которого находится в точке 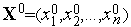, то координаты вершин такого симплекса удобно задавать с помощью 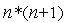матрицы

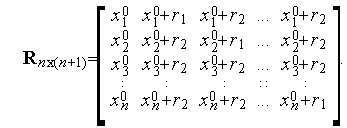(2)

Здесь 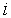-й столбец представляет собой координаты 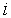-й вершины симплекса, ;

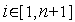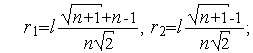(3)

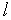-длина ребра симплекса.

Например, регулярный симплекс в двумерном пространстве 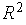с одной из вершин в начале координат (когда 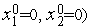определяется 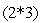матрицей

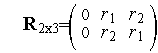
и имеет вид, представленный на рис. 1.

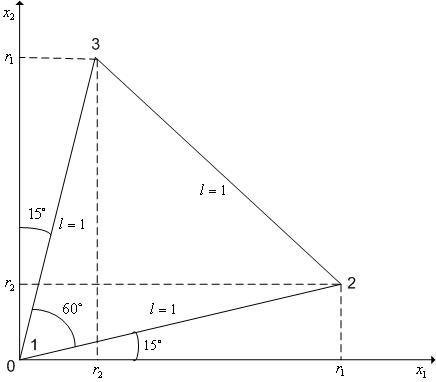Рис. 1. Регулярный симплекс в пространстве R ² с одной из вершин в начале координат.

В алгоритме симплекс-метода используется следующее важное свойство регулярного симплекса: если одну из вершин регулярного симплекса перенести на надлежащее расстояние вдоль прямой, соединяющей данную вершину и центр тяжести оставшихся вершин, то вновь получится регулярный симплекс (см. рис. 2).

Будем называть эту процедуру отражением вершины симплекса относительно центра тяжести остальных вершин.

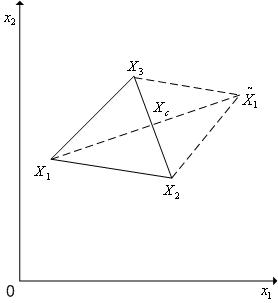Рис. 2. Отражение вершины X ₁ регулярного симплекса в пространстве R ² относительно центра тяжести X _c остальных вершин.

Пусть 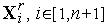- векторы координат вершин регулярного симплекса. Тогда при выполнении операции отражения 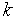-й вершины симплекса имеет место следующая связь координат этой вершины и новой вершины:

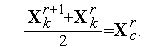(4)

Здесь

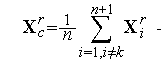(5)

вектор координат центра тяжести остальных вершин симплекса (за исключением отраженной вершины )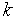

Таким образом, после отражения 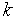-й вершины симплекса с координатами вершин 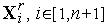, получаем новый симплекс с координатами вершин

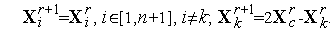(6)

Кроме операции отражения вершины симплекса симплекс-метод может использовать операцию редукции симплекса (см. рис. 3) - уменьшение длин всех ребер симплекса на одну и ту же величину.

Рис. 3. Редукция вершин регулярного симплекса в пространстве R ² к вершине X ₁.

Пусть 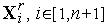- векторы координат вершин регулярного симплекса. Тогда при выполнении операции редукции вершин этого симплекса к вершине новые координаты остальных вершин симплекса определяются по формуле

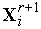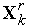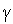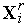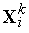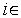= + ( - ), [1, +1], ,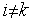

где 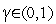- коэффициент редукции. Рекомендуется использовать .

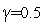Таким образом, после редукции вершин симплекса 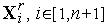к вершине 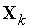получаем новый симплекс с координатами вершин

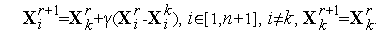(7)

Схема простейшего варианта симплекс-метода.

Суть симплекс-метода раскрывает его простейший вариант.

1. Задаем начальную точку 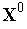, длину ребра симплекса 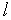и полагаем =0.

2. По формулам (2), (3) находим координаты 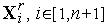всех вершин симплекса.

3. Вычисляем значения минимизируемой функции во всех вершинах симплекса.

4. Находим максимальное из значений функции 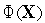в вершинах симплекса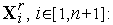

5. По формулам (5), (6) отражаем вершину 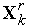относительно центра тяжести остальных вершин симплекса – получаем новый симплекс с координатами вершин .

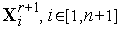6. Вычисляем значение 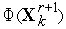минимизируемой функции в новой вершине симплекса.

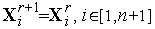7. Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного значения точки минимума функции () принимаем ту вершину симплекса , в которой () имеет минимальное значение, и заканчиваем вычисления. Иначе полагаем = +1 и переходим к п. 4

Поскольку размер симплекса в простейшем варианте симплекс-методе фиксирован, в качестве условия окончания итераций в данном случае можно использовать условие

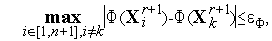(8)

где 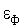- требуемая точность решения по 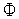, 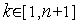- номер произвольной вершины симплекса. Отметим, что выражение в левой части неравенства (8) есть максимальная разность значений функции () в двух вершинах симплекса .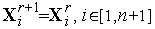

Простейший вариант симплекс-метода иллюстрирует рис. 4, на котором показаны линии уровня функции Химмельблау ( =2).

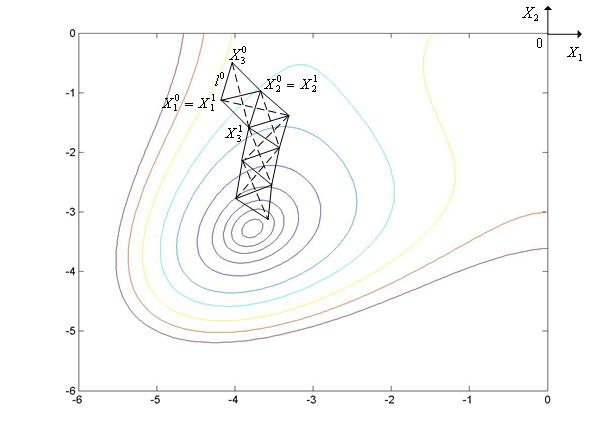Рис. 4. Траектория поиска минимума функции Химмельблау простейшим симплекс-методом.

Модифицированный симплекс-метод.

Рассмотренный простейший симплекс-метод склонен к зацикливанию и медленно сходится, если длина ребра симплекса 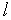выбрана малой (выбор же большой длины ребра симплекса обеспечивает высокую скорость сходимости, но дает малую точность решения). Поэтому в вычислительной практике используются различные модификации простейшего метода, направленные на преодоление его указанных недостатков.

Основной идей модифицированного симплекс-метода является изменение по некоторому правилу размера симплекса в процессе поиска. При этом наряду с условием (8) в качестве условия окончания итераций можно использовать условие

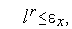(9)

где 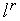- текущая длина ребра симплекса, 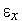- требуемая точность решения по .

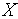Обычно размер симплекса изменяется при выполнении следующих условий:

• при «накрытии» симплексом дна оврага или точки минимума;
• при циклическом движении.

«Накрытие» симплексом дна оврага или точки минимума. Пусть 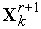- вершина, которая получилась на -ой итерации в результате отражения вершины 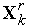. Так что координаты вершин нового симплекса равны .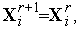

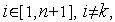
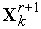Ситуация 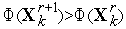интерпретируется как «накрытие» этим симплексом дна оврага или точки минимума и простейший симплекс-метод модифицируется следующим образом (см. рис. 5):

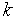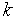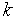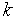1. Полагаем = +1 (если = +2, то полагаем =1);

2. Выполняем отражение 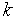-ой вершины симплекса ;

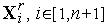3. Если (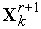)> (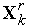) и не все вершины перебраны, то переходим к п.1.

4. Иначе - продолжаем итерации по схеме простейшего симплекс-метода

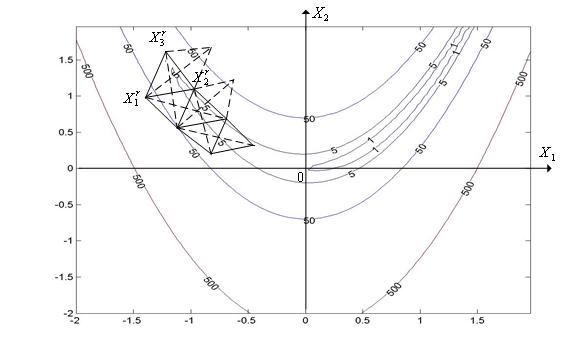Рис. 5. Траектория поиска минимума функции Розенброка модифицированным симплекс-методом при «накрытии» дна оврага. Пунктиром показаны отвергнутые симплексы.

Циклическое движение. Ситуация, когда некоторая вершина симплекса не исключается на протяжении итераций, интерпретируется как «зацикливание» алгоритма. Простейший симплекс-метод модифицируется в этом случае следующим образом:

1. Находим вершину текущего симплекса , в которой функция () принимает наименьшее значение

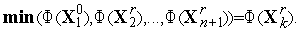
2. По формуле (7) выполняем редукцию симплекса 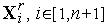к вершине .

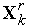3. Продолжаем итерации по схеме простейшего симплекс-метода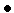

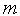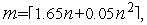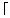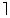Здесь количество итераций рекомендуется находить из условия где * - символ ближайшего целого большего.

6.6 Метод деформируемого многогранника (Нелдера-Мида)

Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в -мерном евклидовом пространстве ,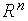

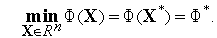(1)

В случае если функция () является овражной функцией, эффективность симплекс-метода при решении задачи (1) значительно снижается в силу того, что регулярный симплекс нельзя «вытянуть» вдоль оврага. Метод Нелдера-Мида (метод деформируемого многогранника) является развитием симплекс-метода и использует в процессе поиска деформацию (изменение размеров и формы) текущего симплекса (не обязательно регулярного).

Метод использует следующие операции над симплексами:

• отражение;
• редукция;
• сжатие;
• растяжение.

Отражение вершины симплекса относительно центра тяжести остальных вершин (см. параграф 5, рис. 1). В результате отражения 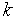-й вершины симплекса с координатами вершин 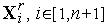, получаем новый симплекс с координатами вершин

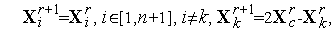(2)

где

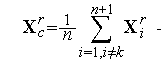(3)

вектор координат центра тяжести остальных вершин симплекса (за исключением отраженной вершины ).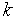

Рис. 1. Отражение вершины X ₁ симплекса в пространстве R ² относительно центра тяжести X _c остальных вершин.

Редукции симплекса (см. параграф 5, рис. 2) - уменьшение длин всех ребер симплекса в одно и то же количество раз. В результате выполнения редукции вершин симплекса 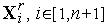к вершине 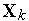получаем новый симплекс с координатами вершин

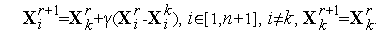(4)

где 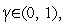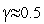- коэффициент редукции.

Рис. 2. Редукция вершин симплекса в пространстве R ² к вершине X ₁.

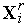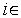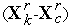Сжатие симплекса (см. рис. 3). В результате выполнения сжатия симплекса , [1, +1] в направлении получаем новый симплекс с координатами вершин

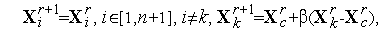(5)

где 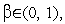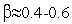- коэффициент сжатия, 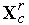- вектор координат центра тяжести остальных вершин симплекса (см. (3)).

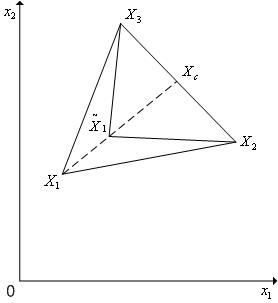Рис. 3. Сжатие симплекса в пространстве R ² в направлении (X ₁- X _c).

Растяжение симплекса (см. рис. 4). В результате выполнения растяжения симплекса 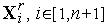в направлении 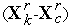получаем новый симплекс с координатами вершин

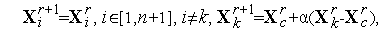(6)

где 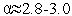- коэффициент растяжения, 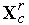- вектор координат центра тяжести остальных вершин симплекса (см. (3)).

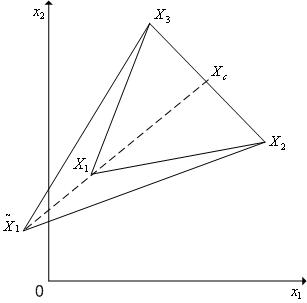Рис. 4. Растяжение симплекса в пространстве R ² в направлении (X ₁- X _c).

Схема метода Нелдера-Мида.

Симплекс с вершинами 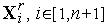обозначим .

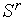1. Задаем начальную точку 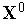, длину ребра симплекса 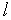и полагаем =0.

2. Находим координаты 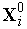, 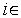[1, +1] всех вершин регулярного симплекса 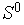с длиной ребра 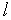. Вычисляем значения (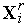) минимизируемой функции во всех вершинах симплекса.

3. Среди вершин симплекса 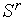находим вершины 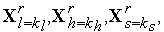в которых функция () принимает, соответственно, наименьшее, наибольшее и следующее за максимальным значения, а также находим значения функции () в этих точках:

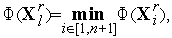
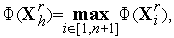
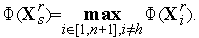
4. По формулам (2), (3) выполняем отражение вершину симплекса 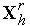относительно центра тяжести остальных вершин симплекса – получаем новый симплекс 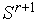. Вычисляем значение (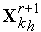) минимизируемой функции в новой вершине симплекса.

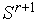5. Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного значения точки минимума функции () принимаем ту вершину симплекса , в которой () имеет минимальное значение, и заканчиваем вычисления.

6. Есл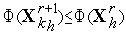и и 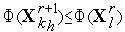, то переходим к п.7 (растяжению симплекса) - см. рис. 5. Если 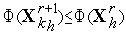, но 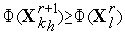, то переходим к п.3 (отражению) – см. рис. 6. Если 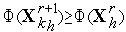, то переходим к п.8 (сжатию симплекса) – см. рис. 7, рис. 8.

7. Ситуация 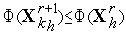и 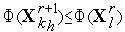. По формуле (6) выполняем растяжение симплекса 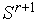в направлении 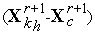- получаем новый симплекс 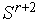. Вычисляем значение минимизируемой функции в новой вершине симплекса 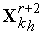. Если 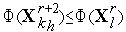, то полагаем 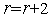и переходим к п.3 (отражению вершины симплекса). Иначе полагаем 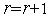и переходим к п.3 (отражению вершины симплекса) с симплексом 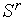(т.е. не используем результаты растяжения).

8. Ситуация 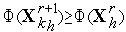. По формуле (5) выполняем сжатие симплекса 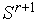в направлении 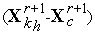- получаем новый симплекс 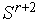. Вычисляем значение минимизируемой функции в новой вершине симплекса 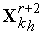. Если 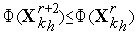, то полагаем = +2 и переходим к п.3 (отражению вершины симплекса). Иначе по формуле (4) выполняем редукцию симплекса 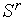к вершине 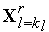- получаем новый симплекс 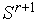. Вычисляем значение минимизируемой функции во всех новых вершинах симплекса 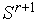. Полагаем = +1 и переходим к п.3 (отражению симплекса)

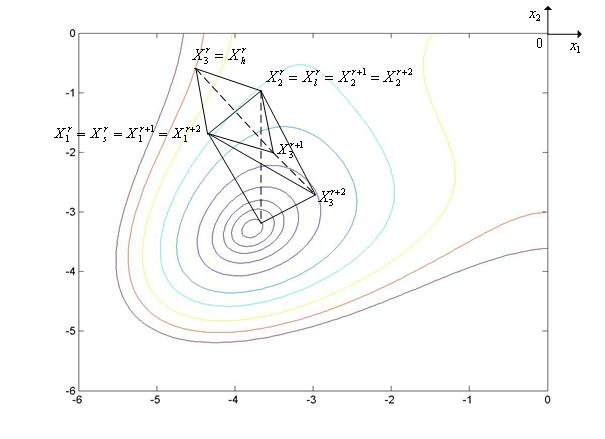Рис. 5. Ситуация, когда метод Нелдера-Мида использует успешное растяжение симплекса.

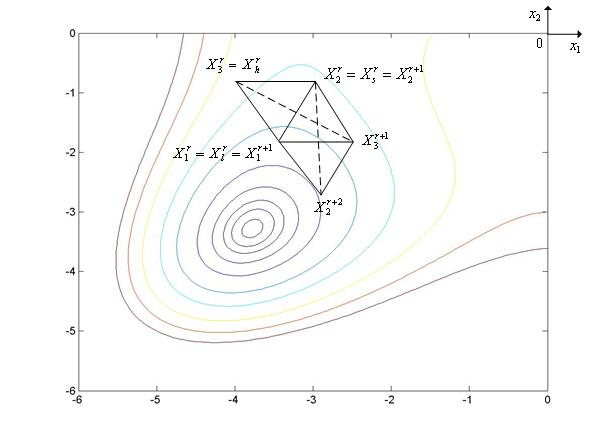Рис. 6. Ситуация, когда метод Нелдера-Мида использует успешное отражение симплекс.

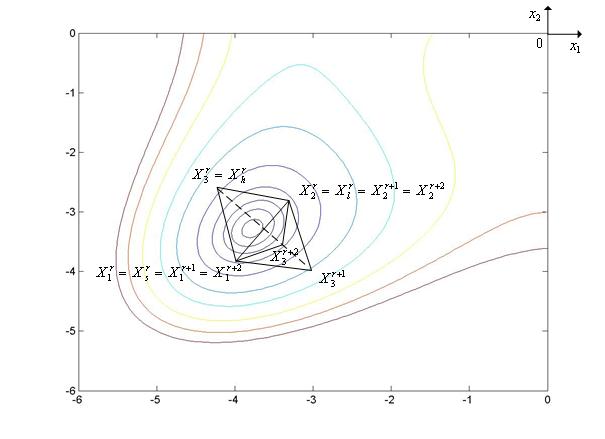Рис. 7. Ситуация, когда метод Нелдера-Мида использует успешное сжатие симплекс.

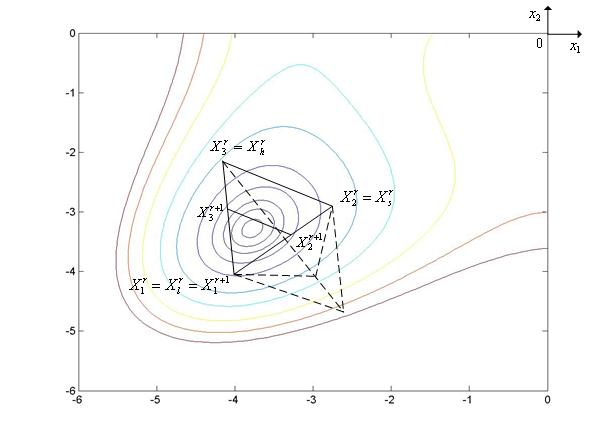Рис. 8. Ситуация, когда метод Нелдера-Мида использует редукцию после неудачного сжатия симплекса. Пунктиром показаны отвергнутые (неудачные) итерации.

На рис. 5 - рис. 8 минимизируемой функцией () является функция Химмельблау.

В качестве условия окончания итераций в методе Нелдера-Мида можно использовать условие

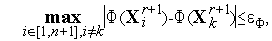
где 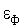- требуемая точность решения по 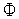, 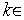[1, +1] - номер произвольной вершины симплекса. Можно также завершать итерации, когда длина максимального из ребер текущего симплекс станет меньше или равна 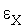- требуемой точности решения по .

Изложенная схема метода Нелдера–Мида имеет тот недостаток, что для сильно овражных функций может происходить вырождение («сплющивание») симплекса. Поэтому к рассмотрен