Итерационная формула. Итерация градиентного метода с дроблением шага для задачи (10), (11) имеет вид

Итерация градиентного метода с дроблением шага для задачи (10), (11) имеет вид

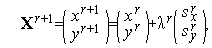
(12)

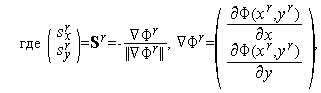
(13)

а величина шага 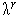находится из условия

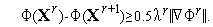
(14)

Найдем явные выражения для частных производных функции (11):

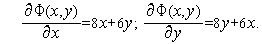
(15)

Таким образом, из (12), (13), (15) имеем искомую итерационную формулу градиентного метода с дроблением шага для задачи (10), (11).

=- , =- ,

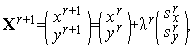
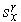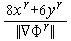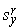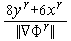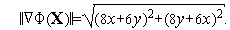
(16)

3.Первая итерация ( 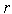=0).

Из формул (15), (16) последовательно имеем

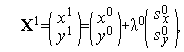
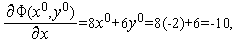
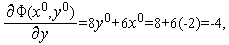
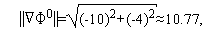
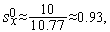
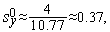
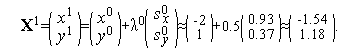
Таким образом, 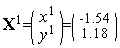(см. рис. 3).

Условие (14) на первой итерации имеет вид

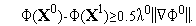
Поскольку

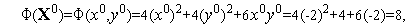
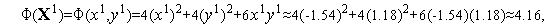
левая часть этого неравенства равна 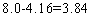. Его правая часть, легко видеть, равна .

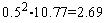Таким образом, на первой итерации условие (14) выполняется и величина шага 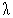должна быть изменена: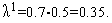

4.Вторая итерация ( 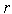=1).

Аналогично первой итерации последовательно имеем

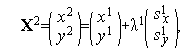
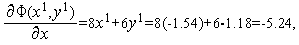
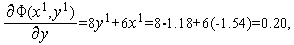
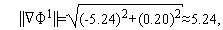
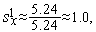
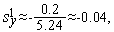
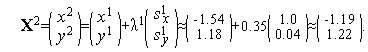
Таким образом, 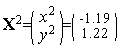(см. рис. 3).

Условие (14) на второй итерации имеет вид

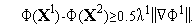
Поскольку

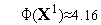
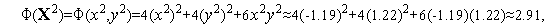
левая часть этого неравенства равна 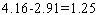. Его правая часть, легко видеть, равна .

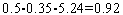Таким образом, на второй итерации условие (14) выполняется и величина шага 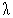должна быть изменена: .

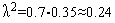5.Третья итерация ( 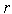=2).

Аналогично первой итерации последовательно имеем

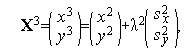
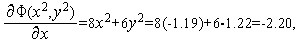
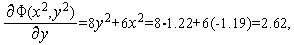
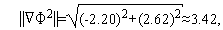
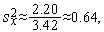
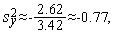
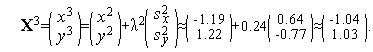
Таким образом, 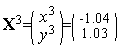(см. рис. 3).

Условие (14) на третьей итерации имеет вид

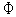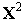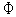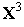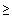()- () 0.5 .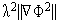

Поскольку

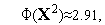
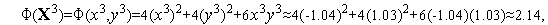
левая часть этого неравенства равна 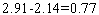. Его правая часть, легко видеть, равна .

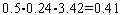Таким образом, на третьей итерации условие (14) выполняется и величина шага 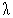должна быть изменена: .

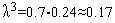Градиентный метод с дроблением шага. Тест 1

Выполните несколько итераций (не менее двух) решения двумерной задачи локальной безусловной оптимизации

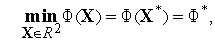
(1)

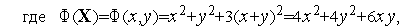
(2)

градиентным методом с дроблением шага, исходя из точки .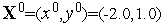

Примите 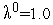, , 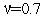в качестве нормы вектора градиента используйте евклидову норму.

Траекторию поиска изобразите на рисунке, на котором приведены линии уровня квадратичной функции (2), которые могут быть получены с помощью следующей MATLAB-программы:

x=-2:0.06:2;

y=x;

[X,Y]=meshgrid(x);

Z=(X).^2+(Y).^2+3*(X+Y).^2;

V=[0.1,0.2,0.4,0.8,1.5,3.,6.,12,24];

[C,h]=contour(X,Y,Z,V);

clabel(C,h);

Ответ