Пусть в области 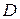 , в которой определена функция
, в которой определена функция 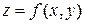 , в некоторой внутренней точке
, в некоторой внутренней точке 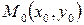 задано направление вектором
задано направление вектором 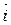 (см. рис.8). Нас интересует поведение функции при движении точки
(см. рис.8). Нас интересует поведение функции при движении точки 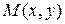 в этом направлении. Пусть
в этом направлении. Пусть 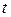 расстояние между точками
расстояние между точками 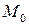 и
и 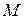 , а
, а 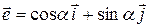 – единичный вектор заданного направления
– единичный вектор заданного направления 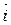 . Тогда координаты точки
. Тогда координаты точки 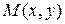 равны:
равны: 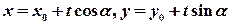 . Если точка
. Если точка  стремится к точке
стремится к точке  в заданном направлении, то
в заданном направлении, то 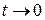 .
.
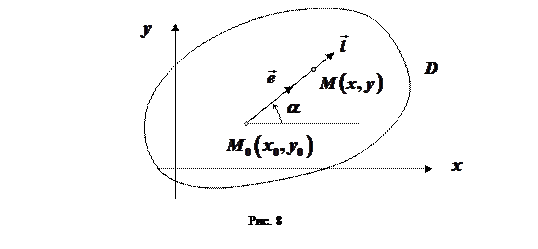
Производной функции 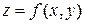 в точке
в точке 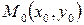 в заданном направлении
в заданном направлении 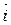 называется предел
называется предел
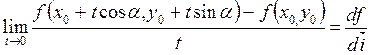 .
.
В частности, частные производные 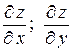 это производные по направлению координатных осей
это производные по направлению координатных осей 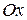 и
и 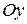 соответственно. Оказывается, что для функции, имеющей непрерывные частные производные, производная по направлению выражается через частные производные в данной точке. Чтобы это доказать, нам необходимо научиться находить частные производные сложных функций.
соответственно. Оказывается, что для функции, имеющей непрерывные частные производные, производная по направлению выражается через частные производные в данной точке. Чтобы это доказать, нам необходимо научиться находить частные производные сложных функций.
Производная 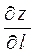 характеризует скорость изменения функции в направлении
характеризует скорость изменения функции в направлении 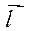 .
.
Теорема. Если функция  дифференцируема в точке
дифференцируема в точке  , то производная
, то производная 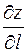 по направлению
по направлению 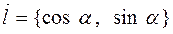 в точке
в точке  определяется формулой
определяется формулой
 ,(1)
,(1)
где 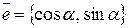 – единичный вектор заданного направления
– единичный вектор заданного направления 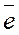
Замечание. Если направление 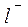 задано вектором
задано вектором 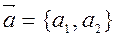 , то производная
, то производная 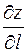 функции
функции  по направлению
по направлению 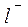 может быть подсчитана по формуле
может быть подсчитана по формуле
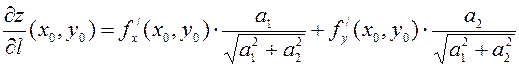 . (2)
. (2)
Пример. Найти производную от функции 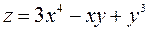 в точке М (1,2) в направлении, составляющим с осью
в точке М (1,2) в направлении, составляющим с осью 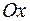 угол в
угол в 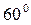 .
.
Решение. Направление задано углом наклона к оси 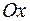 , поэтому воспользуемся формулой (1).
, поэтому воспользуемся формулой (1).
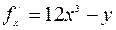 ,
, 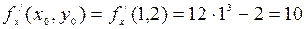 ,
,
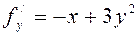 ,
, 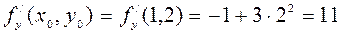 ,
,
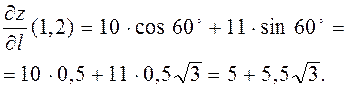
Пример. Найти производную от функции 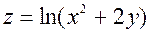 в точке М (1;2) найти производную по направлению
в точке М (1;2) найти производную по направлению 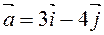 .
.
Решение. Направление задано координатами вектора 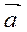 , поэтому воспользуемся формулой (2).
, поэтому воспользуемся формулой (2).
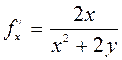 ,
, 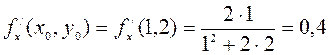 ,
,
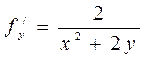 ,
, 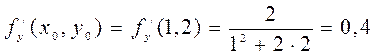 ,
,
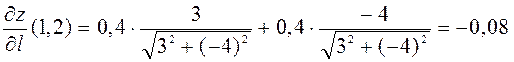 .
.
Рассмотрим понятие градиента функции 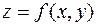 .
.
Градиентом 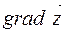 функции
функции  называется вектор с координатами
называется вектор с координатами 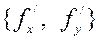 .
.
 2015-03-22
2015-03-22 541
541








