2015-03-22
347
1. Производная функции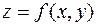 
по направлению 
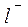есть скалярное произведение градиента 
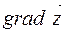и единичного вектора 
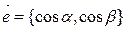, задающего направление .
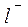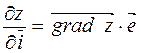
2. Градиент 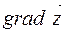функции 
в данной точке характеризует направление максимальной скорости изменения функции в этой точке, причем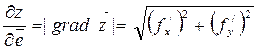 
.
3. Если градиент 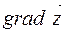дифференцируемой функции в точке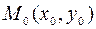 
отличен от нуля, то вектор 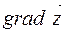перпендикулярен линии уровня, проходящей через данную точку.
Пример. Найти градиент функции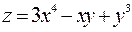 
в точке М (1,2).
Решение. Находим
, 
,
, 
.
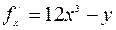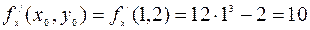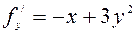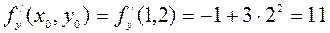Следовательно,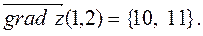 
ЭКСТРЕМУМЫ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Частные производные высших порядков.
