Дифференциалом 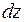 дифференцируемой в точке
дифференцируемой в точке  функции
функции  называется главная линейная часть полного приращения этой функции в точке
называется главная линейная часть полного приращения этой функции в точке  , то есть
, то есть
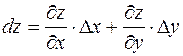 . (1)
. (1)
Если положить 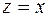 , то
, то 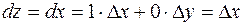 , то есть
, то есть 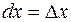 . Аналогично, полагая
. Аналогично, полагая 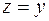 , получим, что
, получим, что 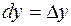 . Таким образом, дифференциалы независимых переменных совпадают с приращениями этих переменных, то есть
. Таким образом, дифференциалы независимых переменных совпадают с приращениями этих переменных, то есть
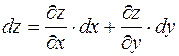 . (2)
. (2)
Геометрический смысл дифференциала: если полное приращение функции 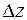 представляет геометрически приращение
представляет геометрически приращение 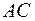 аппликаты поверхности
аппликаты поверхности  , то дифференциал функции
, то дифференциал функции 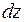 есть приращение
есть приращение 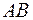 аппликаты касательной плоскости к поверхности
аппликаты касательной плоскости к поверхности  в данной точке, когда переменные
в данной точке, когда переменные 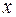 и
и 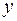 получают приращения
получают приращения 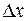 и
и 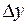 (см. рис.7).
(см. рис.7).
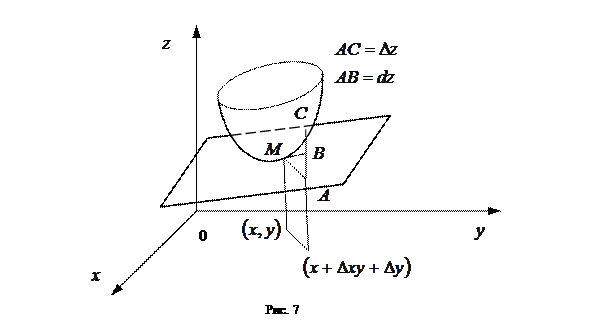
Напомним, что если функция 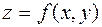 дифференцируема в точке
дифференцируема в точке  , то ее полное приращение в этой точке может быть представлено в виде
, то ее полное приращение в этой точке может быть представлено в виде
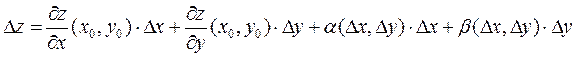 (3)
(3)
Из соотношений (2) и (3) следует, что при достаточно малых 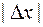 и
и 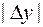 имеет место приближенное равенство
имеет место приближенное равенство 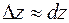 . Отсюда получаем формулу приближенных вычислений:
. Отсюда получаем формулу приближенных вычислений:
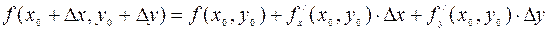 (4)
(4)
Пример. Вычислить приближенно 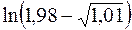 .
.
Решение. Рассмотрим функцию 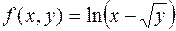 . Тогда
. Тогда 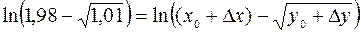 , где
, где 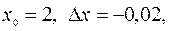 .
. 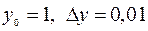 . Воспользуемся формулой (4), предварительно найдя
. Воспользуемся формулой (4), предварительно найдя 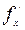 и
и 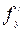 :
:
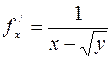 ,
, 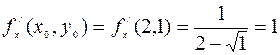 ,
,
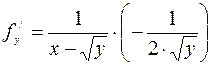 ,
, 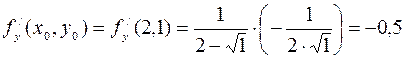 .
.
Следовательно, 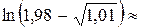
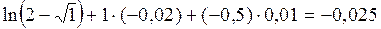 .
.
Для сравнения: используя микрокалькулятор, находим: 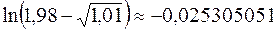 .
.
 2015-03-22
2015-03-22 387
387








