Пусть функция  , дифференцируемая в точке
, дифференцируемая в точке  , задает в пространстве поверхность
, задает в пространстве поверхность 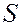 . Пересечем эту поверхность плоскостями
. Пересечем эту поверхность плоскостями 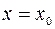 и
и 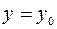 (см. рис.4). Плоскость
(см. рис.4). Плоскость 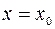 пересекает поверхность
пересекает поверхность 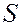 по некоторой линии
по некоторой линии 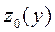 , уравнение которой получается подстановкой в выражение исходной функции
, уравнение которой получается подстановкой в выражение исходной функции  вместо
вместо 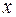 числа
числа 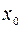 . Точка
. Точка 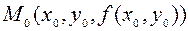 принадлежит кривой
принадлежит кривой 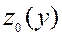 .
.
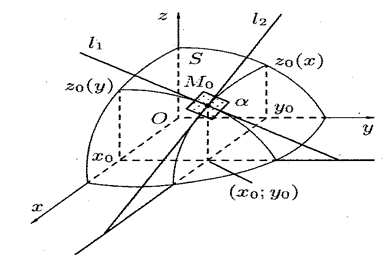
Рис. 6
В силу дифференцируемости функции 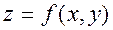 в точке
в точке 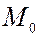 функция
функция 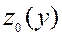 также является дифференцируемой в точке
также является дифференцируемой в точке 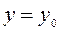 . Следовательно, в этой точке плоскости
. Следовательно, в этой точке плоскости 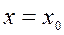 к кривой
к кривой  может быть проведена касательная
может быть проведена касательная 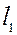 . Проводя аналогичные рассуждения для сечения
. Проводя аналогичные рассуждения для сечения 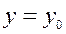 , построим касательную
, построим касательную 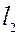 к кривой
к кривой 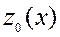 в точке
в точке 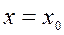 . Прямые
. Прямые 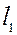 и
и 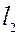 определяют плоскость
определяют плоскость 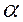 , которая называется касательной плоскостью к поверхности
, которая называется касательной плоскостью к поверхности 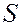 в точке
в точке 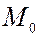 .
.
Прямая, проходящая через точку 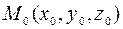 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется нормалью к поверхности в точке
и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется нормалью к поверхности в точке 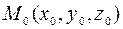 .
.
Теорема. Если функция  дифференцируема в точке
дифференцируема в точке  , то касательная плоскость к поверхности, заданной уравнением
, то касательная плоскость к поверхности, заданной уравнением  , в точке
, в точке 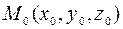 определяется уравнением
определяется уравнением
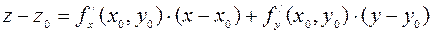 , (1)
, (1)
а нормаль к этой поверхности в заданной точке имеет уравнение
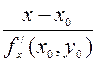 =
= 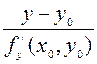 =
= 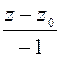 . (2)
. (2)
Если поверхность задана неявно уравнением 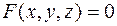 и функция
и функция 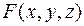 дифференцируема в точке
дифференцируема в точке 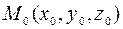 , то касательная плоскость к этой поверхности в точке
, то касательная плоскость к этой поверхности в точке 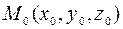 определяется уравнением
определяется уравнением
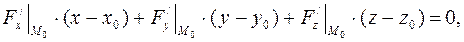 (3)
(3)
а нормаль к этой поверхности в заданной точке имеет уравнение
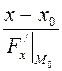 =
=  =
= 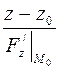 . (4)
. (4)
Замечание. Формулы касательной плоскости и нормали к поверхности получены для обыкновенных, то есть не особых точек поверхности. Точка 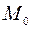 поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.
поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.
Пример. Составить уравнение касательной плоскости и нормали к поверхности: а) 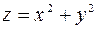 в точке
в точке 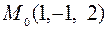 , б)
, б) 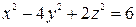 в точке
в точке 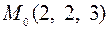 .
.
Решение. а) Поверхность задана явно, поэтому воспользуемся формулами (1), (2). Здесь
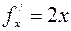 ,
, 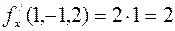 ,
,
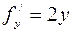 ,
, 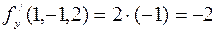 .
.
Тогда искомое уравнение касательной плоскости имеет вид:
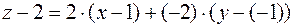 или
или 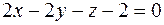
и уравнение нормали:
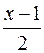 =
= 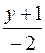 =
= 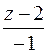 .
.
б) Поверхность задана неявно, поэтому воспользуемся формулами (3), (4). Здесь
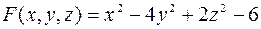 ,
,
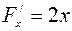 ,
, 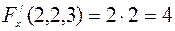 ,
,
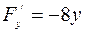 ,
, 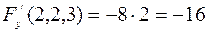 ,
,
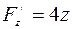 ,
, 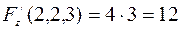 .
.
Тогда искомое уравнение касательной плоскости имеет вид:
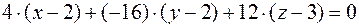
или
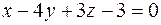
и уравнение нормали: 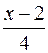 =
= 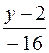 =
= 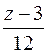 .
.
 2015-03-22
2015-03-22 482
482








