Функция  называется неявной, если она задается уравнением
называется неявной, если она задается уравнением
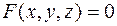 , (1)
, (1)
неразрешенным относительно 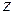 .
.
Найдем частные производные 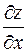 и
и 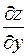 неявной функции
неявной функции 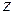 , заданной уравнением (1). Для этого, подставив в уравнение вместо
, заданной уравнением (1). Для этого, подставив в уравнение вместо 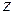 функцию
функцию 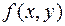 , получим тождество
, получим тождество 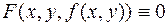 . Частные производные по
. Частные производные по 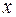 и по
и по 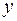 функции, тождественно равной нулю, также равны нулю:
функции, тождественно равной нулю, также равны нулю:
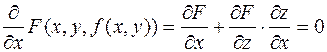 ,
,
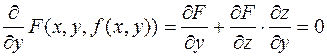 .
.
Откуда
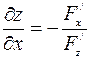 и
и 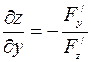 (
(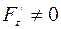 ). (2)
). (2)
Пример. Найти 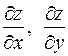 , где
, где 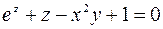 .
.
Решение. Здесь 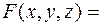
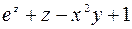 ,
,
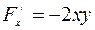 ,
,  ,
, 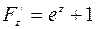 .
.
Тогда по формуле (2) имеем:
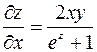 ,
, 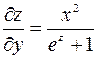 .
.
 2015-03-22
2015-03-22 479
479








