Пусть 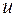 и
и 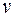 – две любые дифференцируемые функции от
– две любые дифференцируемые функции от 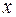 . Тогда дифференциал произведения
. Тогда дифференциал произведения 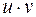 вычисляется по следующей формуле:
вычисляется по следующей формуле:
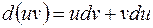 .
.
Отсюда, интегрируя обе части последнего равенства, находим:
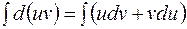 ,
,
или
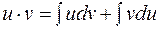 ,
,
откуда
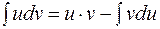 . (4)
. (4)
Полученная формула называется формулой интегрирования по частям для неопределенного интеграла. Она сводит нахождение интеграла 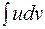 к нахождению интеграла
к нахождению интеграла 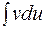 , и если функции
, и если функции 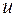 и
и 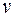 удается подобрать так, чтобы последний интеграл брался проще, чем исходный, то цель будет достигнута.
удается подобрать так, чтобы последний интеграл брался проще, чем исходный, то цель будет достигнута.
Пример. Найти 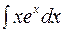 .
.
Решение. Пусть 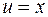 ,
, 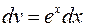 , тогда
, тогда 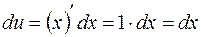 ,
, 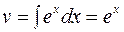 . По формуле (4) находим:
. По формуле (4) находим:
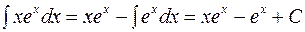 ,
,
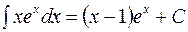 .
.
Пример. Найти 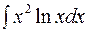
Решение. Пусть 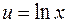 ,
, 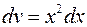 , тогда
, тогда 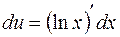 ,
, 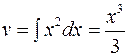 . По формуле (4) находим:
. По формуле (4) находим:
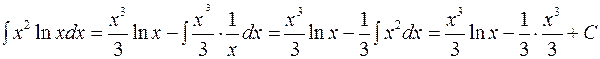 ,
,
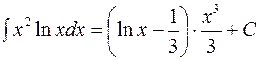 .
.
 2015-03-22
2015-03-22 438
438








