Криволинейной трапецией назовем плоскую геометрическую фигуру, ограниченную двумя прямыми 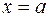 и
и 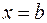
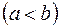 , отрезком
, отрезком 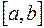 оси
оси 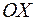 и графиком некоторой непрерывной функции
и графиком некоторой непрерывной функции 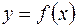 ,
, 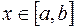
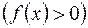 .
.
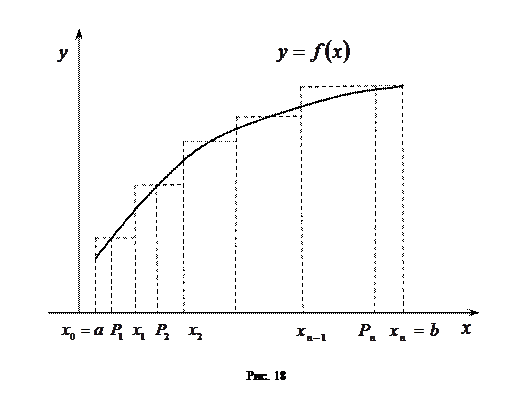
Найдем площадь 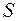 этой фигуры. Для этого:
этой фигуры. Для этого:
1) разобьем отрезок 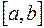 произвольно расположенными, но следующими друг за другом точками
произвольно расположенными, но следующими друг за другом точками 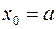 ,
, 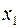 ,
, 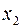 ,...,
,..., 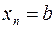 ;
;
2) в каждом из полученных отрезков длины 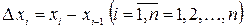 выберем произвольную точку
выберем произвольную точку 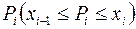 и вычислим значение функции в этих точках
и вычислим значение функции в этих точках 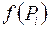
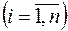 ;
;
3) рассмотрим прямоугольники с основаниями 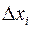 и высотами
и высотами 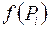
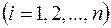 и найдем их площади
и найдем их площади 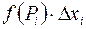
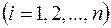 . Сложив эти числа, получим сумму
. Сложив эти числа, получим сумму 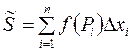 . Значение полученной суммы
. Значение полученной суммы 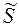 приближенно равно площади
приближенно равно площади 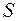 криволинейной трапеции
криволинейной трапеции 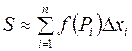 (чем мельче отрезки
(чем мельче отрезки 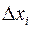
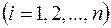 , тем лучше будет это приближение).
, тем лучше будет это приближение).
4) введем обозначение: 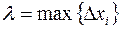 . Для получения точного выражения площади
. Для получения точного выражения площади 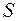 криволинейной трапеции надо перейти к пределу в полученной сумме
криволинейной трапеции надо перейти к пределу в полученной сумме 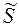 при
при 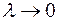 и
и 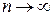 , т.е.
, т.е.
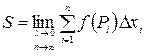 .
.
 2015-03-22
2015-03-22 542
542








