2015-03-22
463
Во многих случаях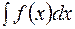 
можно упростить, если вместо 
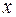ввести новую переменную 
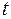, положив
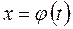, (2)
тогда
.
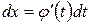Для приведения данного интеграла к новой переменной достаточно привести к новой переменной его подынтегральное выражение
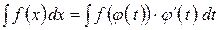, (3)
где
,
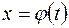в справедливости чего легко убедиться, продифференцировав обе части равенства (3) и воспользовавшись затем формулами (1) и (2).
Метод подстановки, или, как его также называют, метод замены переменной интегрирования, является одним из наиболее эффективных и распространенных методов интегрирования. С другой стороны, не существует общих правил, которые во всех случаях позволяли бы найти подстановку, ведущую к желаемой цели. Поэтому, чем больше примеров самостоятельно решить, тем с большим успехом можно овладеть методом подстановки.
Пример. Найти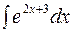 
.
Решение. Данный интеграл не табличный, но есть интеграл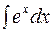 
, сходный с данным. Поэтому введем новую переменную 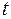, связанную с 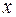зависимостью: 
, 
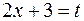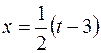. Дифференцируя это равенство, получим: 
, 
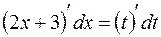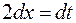, откуда 
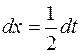. Подставив результат в данный интеграл, имеем:
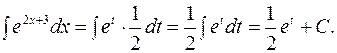
Возвращаясь к переменной 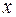, находим:
.
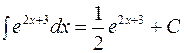Для надежности проверяем результат дифференцированием:
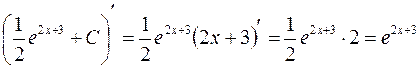– верно.
