Если уравнение заданной линии есть 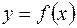 , то, как было показано, площадь
, то, как было показано, площадь 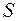 криволинейной трапеции определяется формулой:
криволинейной трапеции определяется формулой:
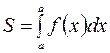 .
.
Обобщим полученные результаты на случай вычисления площади произвольной плоской фигуры.
Площадь 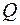 , ограниченная кривыми
, ограниченная кривыми 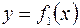 и
и 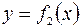 и прямыми
и прямыми 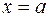 ,
, 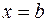 , при условии
, при условии 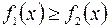 , будет, очевидно, равна разности площадей криволинейных трапеций
, будет, очевидно, равна разности площадей криволинейных трапеций 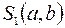 и
и 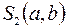 , то есть
, то есть
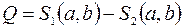 ,
,
или
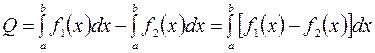 . (2.7)
. (2.7)
Пример. Вычислить площадь, ограниченную кривыми 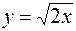 и
и 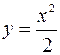 .
.
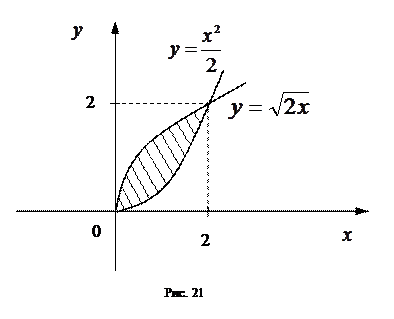
Решение. Находим абсциссыточек пересечения заданных кривых:
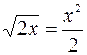 ;
; 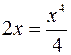 ;
; 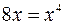 ;
; 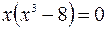 , откуда
, откуда 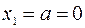 ,
, 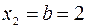 . Следовательно, в соответствие с формулой (2.7)
. Следовательно, в соответствие с формулой (2.7) 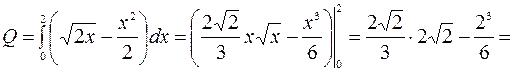
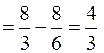 (кв. ед.)
(кв. ед.)
Ответ: 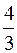 кв.ед.
кв.ед.
Контрольные задания
Задание № 1
Найти уравнения и построить линии уровня функции 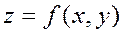 :
:
1.1 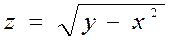 .
.
1.2 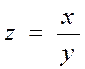 .
.
1.3 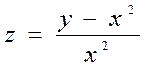 .
.
1.4 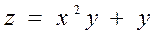 .
.
1.5 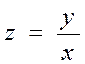 .
.
1.6 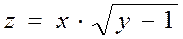 .
.
1.7 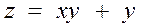 .
.
1.8 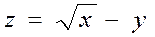 .
.
1.9 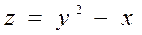 .
.
1.10 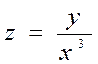 .
.
 2015-03-22
2015-03-22 605
605








