Формула Ньютона-Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции.
Теорема. Если 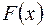 – одна из первообразных непрерывной на отрезке
– одна из первообразных непрерывной на отрезке 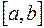 функции
функции 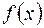 , то справедлива следующая формула Ньютона-Лейбница:
, то справедлива следующая формула Ньютона-Лейбница:
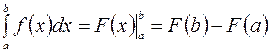 . (4.1)
. (4.1)
Доказательство. Доказательство проведем, используя свойство 7. обозначим определенный интеграл с переменным верхним пределом 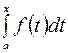 через функцию
через функцию 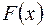 , т.е.
, т.е. 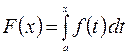 . Тогда в силу свойства 7 можно записать
. Тогда в силу свойства 7 можно записать 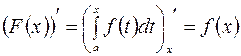 . Следовательно,
. Следовательно, 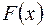 является одной из первообразных для интеграла
является одной из первообразных для интеграла 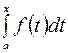 . Так как, все первообразные отличаются на постоянную, то имеет место равенство
. Так как, все первообразные отличаются на постоянную, то имеет место равенство 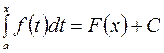 ,
, 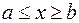 , где
, где 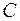 – некоторое число. Подставляя в это равенство значение
– некоторое число. Подставляя в это равенство значение 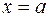 , имеем
, имеем 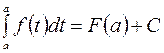
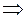
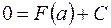
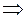
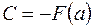 , т.е. длялюбого
, т.е. длялюбого 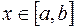 имеем
имеем 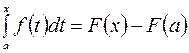 . Полагая
. Полагая 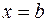 , получаем соотношение
, получаем соотношение 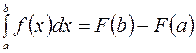 . Обозначим разность
. Обозначим разность 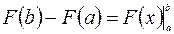 . Тогда формулу Ньютона-Лейбница можно записать в виде
. Тогда формулу Ньютона-Лейбница можно записать в виде 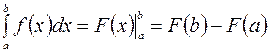 . Теорема доказана.
. Теорема доказана.
Замечание. Из формулы Ньютона-Лейбница следует, что при вычислении определенного интеграла надо найти первообразную 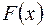 для подынтегральной функции
для подынтегральной функции 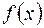 и вычислить разность
и вычислить разность 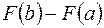 . Следовательно, формально все сводится к вычислению неопределенного интеграла, и здесь применимы все методы вычисления неопределенного интеграла.
. Следовательно, формально все сводится к вычислению неопределенного интеграла, и здесь применимы все методы вычисления неопределенного интеграла.
Пример. Вычислить 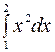 .
.
Решение. Взяв неопределенный интеграл 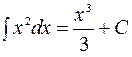 и воспользовавшись формулой (4.1), решаем:
и воспользовавшись формулой (4.1), решаем:
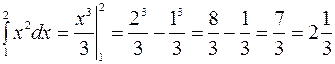 .
.
Ответ: 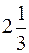 .
.
 2015-03-22
2015-03-22 2208
2208
