Для вычисления определенного интеграла подстановкой поступают так же, как и при нахождения неопределенного интеграла подстановкой. Но при этом есть одна особенность, суть которой заключается в том, что неопределенный интеграл есть функция, а определенный интеграл есть число.
Как было показано в примере 3, для того, чтобы при помощи подстановки привести заданный неопределенный интеграл к табличному, аргумент выражают через новую переменную, затем находят неопределенный интеграл, и полученный результат снова выражают через первоначальный аргумент. В случае же определенного интеграла нет необходимости возвращаться к первоначальной переменной.
Таким образом, для вычисления определенного интеграла подстановкой пользуются формулой:
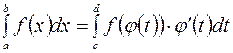 , (4.2)
, (4.2)
где 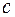 и
и 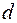 , отличные от
, отличные от 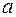 и
и 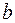 пределы интегрирования, находятся из подстановки
пределы интегрирования, находятся из подстановки 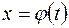 , т. е.
, т. е. 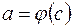 ,
, 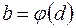 .
.
Пример. Вычислить 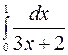 .
.
Решение. Заменяя 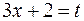 , находим
, находим 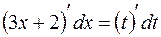 , или
, или 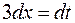 , откуда
, откуда 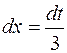 . Найдем новые пределы интегрирования по формуле:
. Найдем новые пределы интегрирования по формуле: 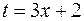 .
.
Нижний предел 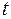 при
при 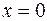 равен:
равен: 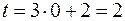 , а верхний предел
, а верхний предел 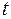 при
при 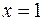 равен:
равен: 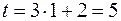 .
.
Тогда вычисление данного интеграла запишется так:
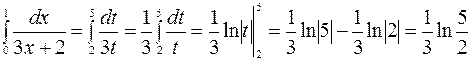 .
.
Ответ: 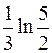 .
.
 2015-03-22
2015-03-22 3696
3696
