2015-03-22
484
Для функции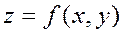 
в точке 
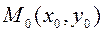найти: а) градиент, б) производную по направлению вектора 
.
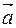2.1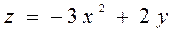 
, 
, 
.
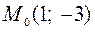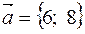2.2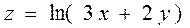 
, 
, 
.
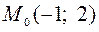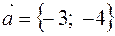2.3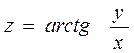 
, 
, 
.
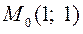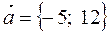2.4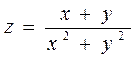 
, 
, 
.
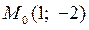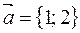2.5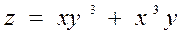 
, 
, 
.
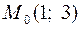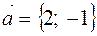2.6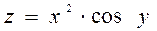 
, 
, 
.
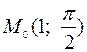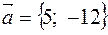2.7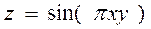 
, 
, 
.
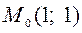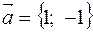2.8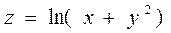 
, 
, 
.
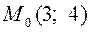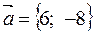2.9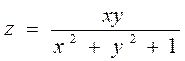 
, 
, 
.
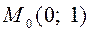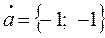2.10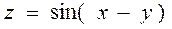 
, 
, 
.
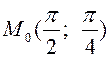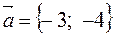Задание № 3
Составить уравнение касательной плоскости и нормали к поверхности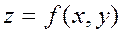 
в точке 
:
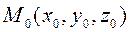3.1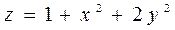 
, 
.
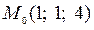3.2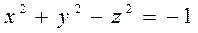 
, 
.
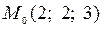3.3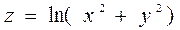 
, 
.
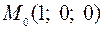3.4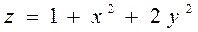 
, 
.
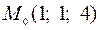3.5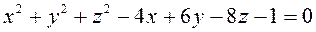 
, 
.
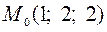3.6 
, 
.
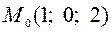3.7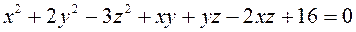 
, 
.
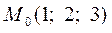3.8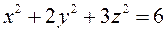 
, 
.
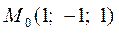3.9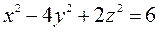 
, 
.
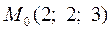3.10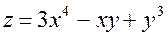 
, 
.
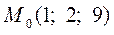Задание № 4
С помощью дифференциала найти приближенное значение числового выражения:
4.1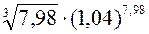 
.
4.2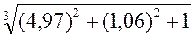 
.
4.3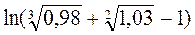 
.
4.4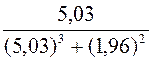 
.
4.5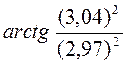 
.
4.6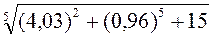 
.
4.7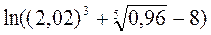 
.
4.8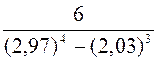 
.
4.9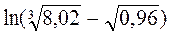 
.
4.10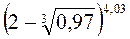 
.
Задание № 5
Для функции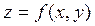 
найти точки экстремума.
5.1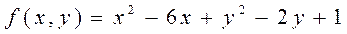 
.
5.2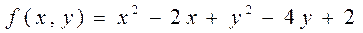 
.
5.3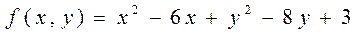 
.
5.4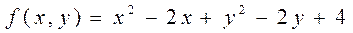 
.
5.5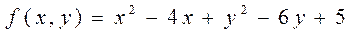 
.
5.6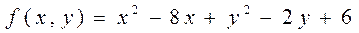 
.
5.7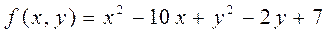 
.
5.8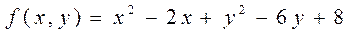 
.
5.9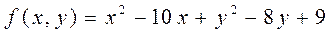 
.
5.10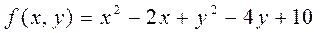 
.
Задание № 6
Найти наибольшее и наименьшее значение функции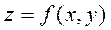 
в замкнутой области 
.
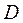6.1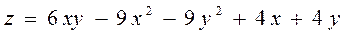 
,
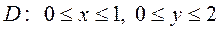
6.2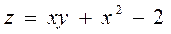 
,
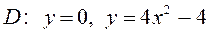
6.3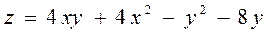 
,
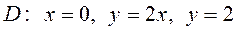
6.4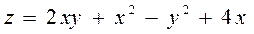 
,
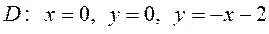
6.5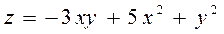 
,
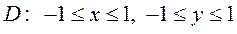
6.6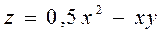 
,
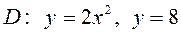
6.7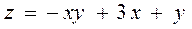 
,
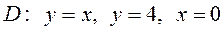
6.8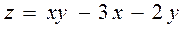 
,
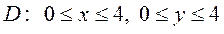
6.9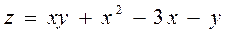 
,
6.10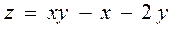 
,
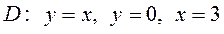
Задание 7
Найти неопределенные интегралы.
| 7.01. | а)  ;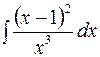
| б)  ;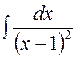
| в)  .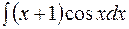
|
| 7.02. | а)  ;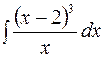
| б)  ;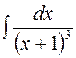
| в)  .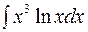
|
| 7.03. | а)  ;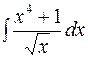
| б)  ;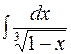
| в)  .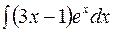
|
| 7.04. | а)  ;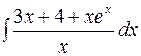
| б)  ;
| в)  .
|
| 7.05. | а)  ;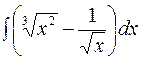
| б)  ;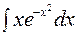
| в)  .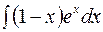
|
| 7.06. | а)  ;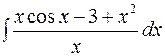
| б)  ;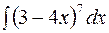
| в)  .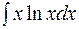
|
| 7.07. | а)  ;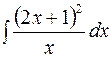
| б)  ;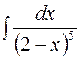
| в)  .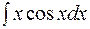
|
| 7.08. | а)  ;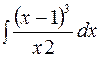
| б)  ;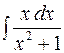
| в) .
|
| 7.09. | а)  ;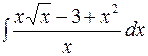
| б)  ;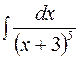
| в)  .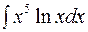
|
| 7.10. | а)  ;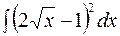
| б)  ;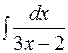
| в)  .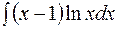
|
Задание 8.
Вычислить площадь фигуры, ограниченной линиями:
|
|
|
| 8.01 |  ;  .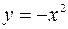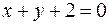
|
| 8.02 |  ;  .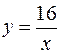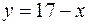
|
| 8.03 |  ;  ;  ;  .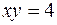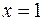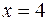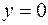
|
| 8.04 |  ;  ; .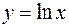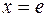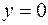
|
| 8.05 |  ; ;  .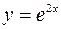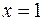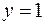
|
| 8.06 |  ;  ;  .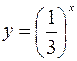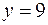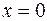
|
| 8.07 |  ;  ; .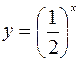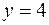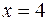
|
| 8.08 |  ; .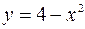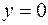
|
| 8.09 |  ; ;  ;  .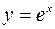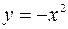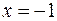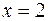
|
| 8.10 |  ; ;  .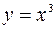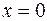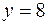
|
Литература
1. Письменный Д.Т. Конспект лекций по высшей математике. - М.: «АЙРИС-ПРЕСС», 2002. –608.с.
2. Важдаев В.П., Коган М.М., Лиогонький М.И., Протасова Л.А 64 лекции по математике. Книга 1 (лекции 1-39): монография; Нижегор. гос. архитектур.-строит. ун-т – Н.Новгород: ННГАСУ, 2012.-284 с.
3. Берман Г.Н. Сборник задач по курсу математического анализа: Учебн. пособие / Г. Н. Берман.- СПб.: «Профессия», 2003. – 432 с.
4. Курганов А.М., Федоров Н.Ф. Справочник по гидравлическим расчетам водоснабжения и канализации. – Л., 1978.
