В задачах 8. 1-8.20 даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точность до двух знаков; 4) уравнение высоты СD и ее длину; 5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой CD; 6) уравнение прямой, проходящей через точку К параллельно стороне АВ; 7) координаты точки М, расположенной симметрично точке А относительно прямой CD.
8.1 А (-8;-3), В (4;-12), С (8;10).
8.2 А (-5;7), В (7;-2), С (11;20).
8.3 А (-12;-1), В (0;-10), С (4;12).
8.4 А (-10;9), В (2;0), С (6;22).
8.5 А (0;2), В (12;-7), С (16;15).
8.6 А (-9;6), В (3;-3), С (7;19).
8.7 А (1;0), В (13;-9), С (17;13).
8.8 А (-4;10), В (8;1), С (12;23).
8.9 А (2;5), В (14;-4), С (18;18).
8.10 А (-1;4), В (11;-5), С (15;17).
8.11 А (-2;7), В (10;-2), С (8;12).
8.12 А (-6;8), В (6;-1), С (4;13).
8.13 А (3;6), В (15;-3), С (13;11).
8.14 А (-10;5), В (2;-4), С (0;10).
8.15 А (-4;12), В (8;3), С (6;17).
8.16 А (-3;10), В (9;1), С (7;15).
8.17 А (4;1), В (16;-8), С (14;6).
8.18 А (-7;4), В (5;-5), С (3;9).
8.19 А (0;3), В (12;-6), С (10;8).
8.20 А (-5;9), В (7;0), С (5;14).
В задачах 8.21-8.25 составить уравнение геометрического места точек, равноудаленных от данной точки А (х1,у1) и данной прямой у=b. Полученное уравнение привести к простейшему виду и затем построить кривую.
8.21 А (2,5), у =1. 8.22 А (3,-4), у =2.
8.23 А (-4,3), у =-1. 8.24 А (-2,-3), у =-1.
8.25 А (1,-1), у =3.
В задачах 8.26-8.30 составить уравнение геометрического места точек, отношение расстояний которых до данной точки А (х1,у1) и данной прямой у=а. Полученное уравнение привести к простейшему виду и затем построить кривую.
8.26 А (6,0), х =1,5, e =2.
8.27 А (3,0), х = 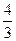 , e =1,5.
, e =1,5.
8.28 А (10,0), х =2,5, e =2.
8.29 А (2,0), х =4,5, e =2/3.
8.30 А (3,0), х =12, e =0,5.
В задачах 8.31-8.35 даны координаты точек А (х1;у1) и В (х2;у2) и радиус окружности R, центр которой находится в начале координат. Требуется: 1) составить каноническое уравнение эллипса, проходящего через данные точки А и В; 2) найти полуоси, фокусы и эксцентриситет этого эллипса; 3) найти все точки пересечения эллипса с данной окружностью; 4) построить эллипс и окружность.
8.31 А (4;-1), В (2; 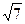 ), R =
), R = 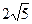 .
.
8.32 А (-8;4), В (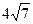 ;-2), R =
;-2), R = 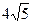 .
.
8.33 А (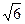 ;-2), В (-3;
;-2), В (-3; 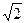 ), R =3.
), R =3.
8.34 А (-6; 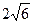 ), В (
), В (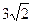 ;6), R =8.
;6), R =8.
8.35 А (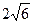 ;-4), В (6;
;-4), В (6; 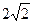 ), R =
), R = 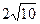 .
.
В задачах 8.36-8.40 даны координаты точек А (х1;у1) и В (х2;у2). Требуется: 1) составить каноническое уравнение гиперболы, проходящей через данные точки А и В, если фокусы гиперболы расположены на оси абсцисс; 2) найти полуоси, фокусы, эксцентриситет и уравнения асимптот этой гиперболы; 3) найти все точки пересечения гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы; 4) построить гиперболу, ее асимптоты и окружность.
8.36 А (-3;4), В (-5; 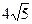 ).
).
8.37 А (4;-6), В (6; 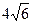 ).
).
8.38 А (-4;-3), В (8;9).
8.39 А (8;12), В (-6; 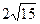 ).
).
8.40 А (8;6), В (10; 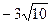 )
)
ТАБЛИЦА ВАРИАНТОВ
 2015-03-22
2015-03-22 1217
1217








