На практике при моделировании реальных производств чаще всего используют два вида производственных функций: линейная и Кобба-Дугласа.
Линейная производственная функция имеет вид:
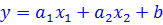
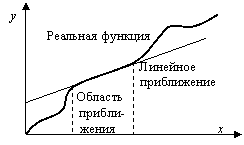
Она строится в случаях, когда объем выпуска пропорционален затратам. Однако данная функция не удовлетворяет первому и третьему требованиям к производственным функциям, поэтому ее можно использовать для приближения реальных функций на небольших локальных участках изменения их аргументов (см. рисунок).
Для выполнения второго требования необходимо выполнение условий
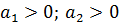
Производственная функция Кобба-Дугласа имеет вид:
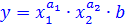
Для выполнения всех требований к производственным функциям необходимо выполнение условий: 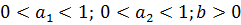
Найдем средние и предельные производительности, эластичности, технологическую норму замены для линейной и Кобба-Дугласа производственных функций.
Для линейной функции 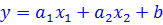 будет:
будет:
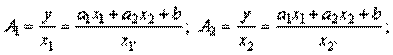
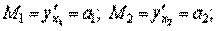
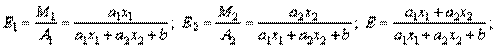
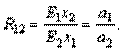
Таким образом, коэффициенты а 1 и а 2 линейной производственной функции имеют смысл предельных производительностей и их можно вычислять по формулам:
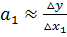
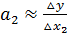
Для производственной функции Кобба-Дугласа 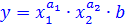 будет:
будет:
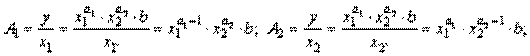
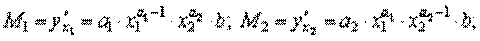

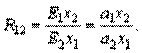
Таким образом, коэффициенты а 1 и а 2 производственной функции Кобба-Дугласа имеют смысл частных эластичностей и их можно вычислять по формулам:
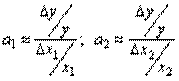
Задача 1. Некоторое предприятие, затрачивая для производства 65 единиц материальных затрат и 17 трудовых, выпускало 120 единиц продукции. В результате расширения и увеличении материальных затрат до 68 единиц выпуск возрос до 124 единиц, а при увеличении трудозатрат до 19 единиц выпуск вырос до 127 единиц. Составить линейную производственную функцию и функцию Кобба-Дугласа.

Решение.
| Записав для удобства исходные данные в виде таблицы и рассчитываем параметры производственных функций. |
Линейная функция y=a1x1+a2x2+b.
· Для нахождения параметров а 1 и а 2 используем формулы:
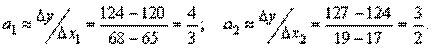
Получаем y=(4/3)x1+(3/2)x2+b.
Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы: 120=(4/3)x1+(3/2)x2+b решаем уравнение относительно b, получаем b=-17,7.
В итоге получаем линейную производственную функцию
y=(4/3)x1+(3/2)x2-17,7.

Производственная функция Кобба-Дугласа имеет вид 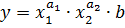 .
.
Находим коэффициенты уравнения:
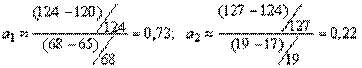 .
.
Получаем уравнение вида 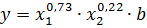 .
.
Для нахождения b подставляем в уравнение исходные данные из 2-го столбца таблицы: 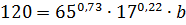 . Вычисляя, получаем b=3,05.
. Вычисляя, получаем b=3,05.
В результате, производственная функция имеет вид:
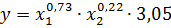

 2015-03-22
2015-03-22 6617
6617
