Итерационные методы решения СЛАУ

Итерационные методы особенно эффективны при большом порядке СЛАУ.

Предварительно приведем систему (4.1) к виду

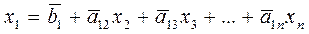, где ,

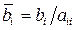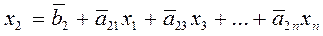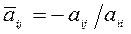, (5.1)

........................

,

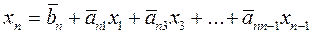Исходя из начального приближения 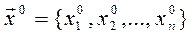, получают векторы 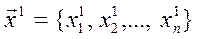,..., 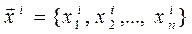по рекурентной формуле

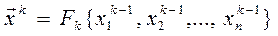. (5.2)

Здесь F_k – некоторая функция, зависящая от матрицы коэффициентов А системы (4.2), правой части 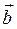, номера приближения k и предыдущих приближений .

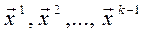Метод имеет 1-й порядок, если F_k не зависит от 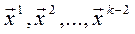, а зависит только от .

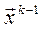Метод стационарный, если F_k не зависит от k.

Простейший случай: если F_k - линейная функция, то общий линейный метод 1 – го порядка должен иметь вид

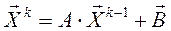(5.3)

Здесь А – квадратная матрица, 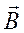- вектор.