Метод Якоби (простой итерации)

К виду (5.3) можно привести, например, выделением диагональных элементов (для i – строки)

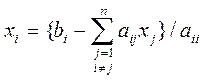, i = 1, 2,..., n (5.4)

Строим последовательность векторов, начиная с произвольного вектора 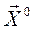(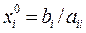, i = 1, 2,..., n)

, ,..., ,

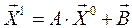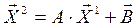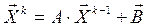где 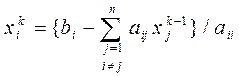, i = 1, 2,..., n (5.5)

Метод Гаусса - Зейделя

В этом методе уточненное значение x₁ сразу же используется для вычисления x₂, а x₁ и x₂ для вычисления x₃ и т.д.

Зададимся начальным приближением неизвестных.

Обычно принимают , ,..., .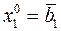

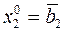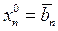Начальные приближения подставляют в 1-е уравнение системы (5.1).

,

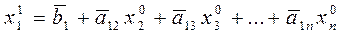затем подставляем 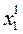, ,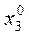..., 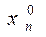во 2-е уравнение

.

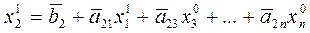Подставляем , , ,...,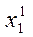

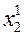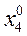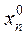
Подставляем 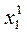, ,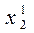..., , 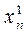выполним 2-ю итерацию.

Приближения с номером k определим по формуле

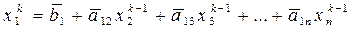
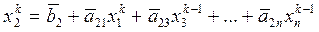(5.6)

...................

,

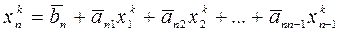Т.е. координаты вектора 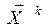определяют по формуле

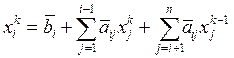, i = 1, 2,..., n (5.7)

Для сходимости метода необходимо, чтобы

1) все диагональные элементы были отличны от 0 (a_ii ≠ 0);

2) диагональные элементы значительно преобладали над остальными коэффициентами матрицы А.

В общем случае критерий окончания итерационного процесса при заданной допустимой погрешности ε > 0 определяется:

- по абсолютным отклонениям в виде

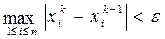, i = 1, 2,..., n (5.8)

- по относительным разностям в виде

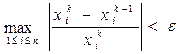
Пример: решить СЛАУ методом Гаусса – Зейделя при ε = 0,01

Предварительно, приводим СЛАУ к виду (5.1)

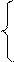2x₁+ x₂+2x₃ =10; 2x₁ = -x₂-2x₃ +10; x₁ = -0,5x₂ - x₃ + 5

x₁+4x₂+ x₃ =12; 4x₂ = -x₁- x₃ +12; x₂ = -0,25x₁- 0,25x₃ + 3

2x₁+2x₂+3x₃ =15; 3x₃ = -2x₁-2x₂+15; x₃ = -0,667x₁-0,667x₂+ 5

Задаем начальные приближения: , , .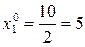

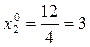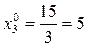Выполняем 1-ю итерацию

1. x₁¹ = - 0,5 ּ3 - 1ּ 5 + 5 = -1,5 Δ₁ =│5 - (-1,5)│= 6,5

x₂¹ = - 0,25 ּ(-1,5) – 0,25 ּ 5 +3 = 2,125 Δ₂ =│3 – 2,13│= 0,87

x₃¹ = - 0,667 ּ(-1,5) – 0,667 ּ2,13 +5 = 4,583 Δ₃ =│5 – 4,583│= 0,417

2. x₁² = - 0,5 ּ2,13 - 1ּ 4,583 + 5 = -0,648 Δ₁ =│-1,5 - (-0,648)│= 0,85

x₂² = -0,25ּ(-0,648) – 0,25ּ4,583 +3 =2,016 Δ₂ =│2,125 – 2,016│= 0,11

x₃² = - 0,667ּ(-0,648) – 0,667ּ2,016+5 =4,088 Δ₃ =│4,583-4,088│= 0,50

3. 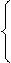x₁³ = -0,095 Δ₁=0,551 4. x₁⁴ = 0,2713 Δ₁=0,37 5. x₁⁵ = 0,514 Δ₁=0,243

x₂³ = 2,002 Δ₂ = 0,014 x₂⁴ = 2,002 Δ₂ = 0,0023 x₂⁵ = 2 Δ₂ = 0,002

x₃³ = 3.728 Δ₃ = 0,358 x₃⁴ = 3,486 Δ₃ = 0,242 x₃⁵ = 3,324 Δ₃ = 0,1621

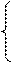
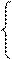
6. 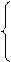x₁⁶ = 0,676 Δ₁=0,16 7 x₁⁷ = 0,784 Δ₁=0,11 8. x₁⁸ = 0,856 Δ₁=0,07

x₂⁶ = 2 Δ₂ = 0 x₂⁷ = 2 Δ₂ = 0 x₂⁸ = 2 Δ₂ = 0

x₃⁶ = 3,216 Δ₃ = 0,108 x₃⁷ = 3,144 Δ₃ = 0,072 x₃⁸ = 3,0964 Δ₃ = 0,048

9. x₁⁹ = 0,903 Δ₁=0,05 10. x₁¹⁰ = 0,936 Δ₁=0,03 11 x₁¹¹ = 0,957 Δ₁=0,02

x₂⁹ = 2 Δ₂ = 0 x₂¹⁰ = 2 Δ₂ = 0 x₂¹¹= 2 Δ₂ = 0

x₃⁹ = 3,064 Δ₃ = 0,032 x₃¹⁰ = 3,043 Δ₃ = 0,02 x₃¹¹ = 3,029 Δ₃ =0,014

12. x₁¹²=0,972 Δ₁=0,014 13. x₁¹³ = 0,981 Δ₁=0,01 14. x₁¹⁴ = 0,99 Δ₁=0,006

x₂¹² = 2 Δ₂ = 0 x₂¹³= 2 Δ₂ = 0 x₂¹⁴ = 2 Δ₂ = 0

x₃¹² =3,019 Δ₃ = 0,010 x₃¹³= 3,013 Δ₃ = 0,006 x₃¹⁴ = 3,006 Δ₃ = 0,004

Точное решение x₁ = 1, x_2, = 2, x₃ = 3.