471-480. Методом Фурье найти уравнение 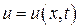 формы однородной струны для любого момента
формы однородной струны для любого момента 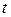 , если струна закреплена на концах
, если струна закреплена на концах 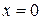 и
и 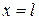 ,
,  а в начальной момент
а в начальной момент 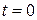 форма струны и скорость точки струны определяются соответственно заданными функциями
форма струны и скорость точки струны определяются соответственно заданными функциями 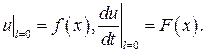
471. 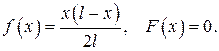
472. 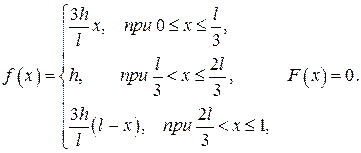
473. 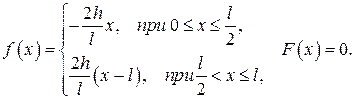
474. 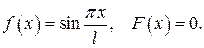
475. 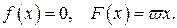
476. 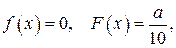 где
где 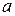 - постоянная, фигурирующая в уравнении струны.
- постоянная, фигурирующая в уравнении струны.
477. 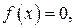
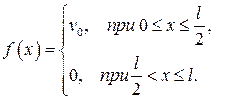
478. 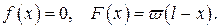
479. 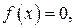
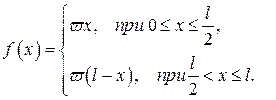
480. 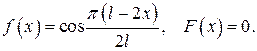
481-490. Восстановить аналитическую в окрестности точки 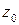 функцию
функцию 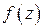 по известной действительной части
по известной действительной части 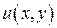 или мнимой
или мнимой 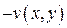 и значению
и значению 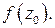
481. 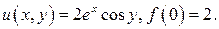 486.
486. 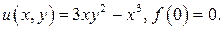
482. 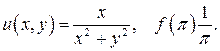 487.
487. 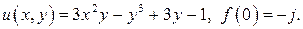
483. 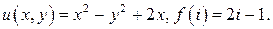 488.
488. 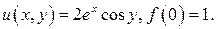
484. 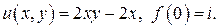 489.
489. 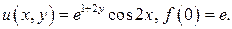
485. 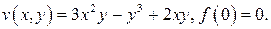 490.
490. 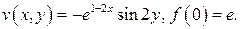
491-500. Разложить функцию 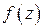 в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки 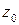 и определить область сходимости этого ряда.
и определить область сходимости этого ряда.
491. 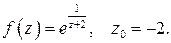 496.
496. 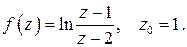
492. 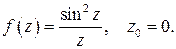 497.
497. 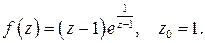
493. 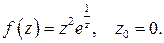 498.
498. 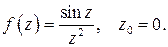
494. 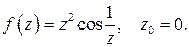 499.
499. 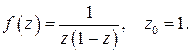
495. 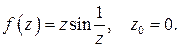 500.
500. 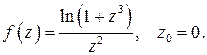
501-510. Используя свойства преобразования Лапласа, найти изображение функции 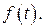
501. 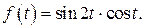 506.
506. 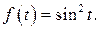
502. 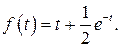 507.
507. 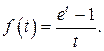
503. 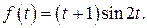 508.
508. 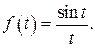
504. 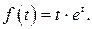 509.
509. 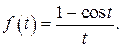
505. 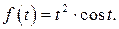 510.
510. 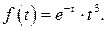
511-520. Найти оригинал по изображению 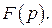
511. 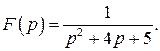 516.
516. 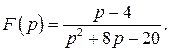
512. 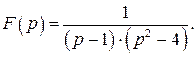 517.
517. 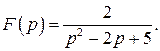
513. 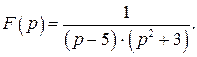 518.
518. 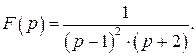
514. 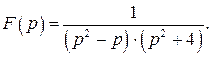 519.
519. 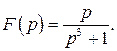
515. 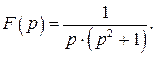 520.
520. 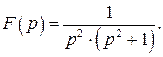
521-530. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.
521. 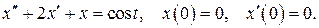
522. 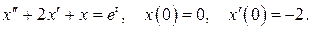
523. 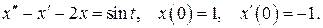
524. 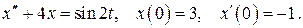
525. 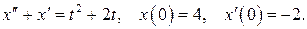
526. 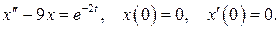
527. 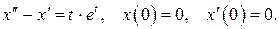
528. 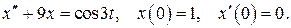
529. 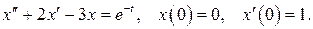
530. 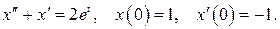
 2015-03-22
2015-03-22 338
338








