281-290. Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
281. а) 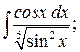

 б)
б) 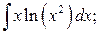
в) 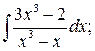 г)
г) 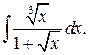
282. а) 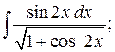 б)
б) 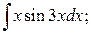
в) 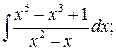 г)
г) 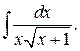
283. а) 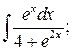 б)
б) 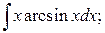
в) 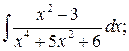 г)
г) 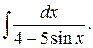
284. а) 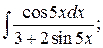 б)
б) 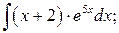
в) 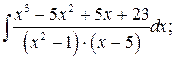 г)
г) 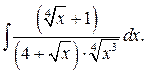
285. а) 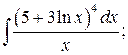 б
б 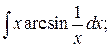
в ) 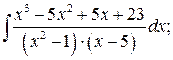 г)
г) 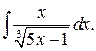
286. а ) 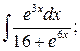 б )
б ) 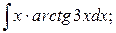
в ) 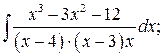 г)
г) 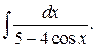
287. а) 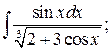 б)
б) 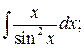
в) 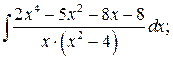 г)
г) 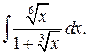
288. а) 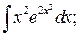 б)
б) 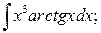
в) 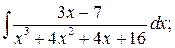 г)
г) 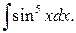
289. а) 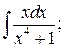 б)
б) 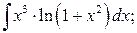
в) 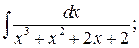 г)
г) 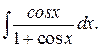
290. а) 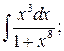 б)
б) 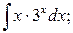
в) 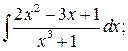 г)
г) 
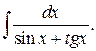
291-300. Вычислить приближенное значение определенного интеграла 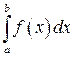 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
291. 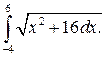 292.
292. 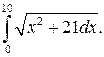
293. 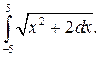 294.
294. 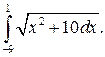
295. 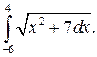 296.
296. 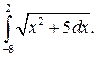
297. 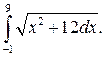 298.
298. 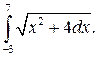
299. 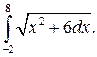 300.
300. 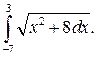
301-310. Вычислить несобственный интеграл или доказать его расходимость.
301. 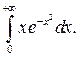 302.
302. 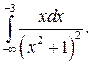
303. 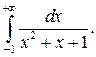 304.
304. 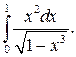
305. 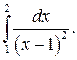 306.
306. 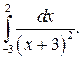
307. 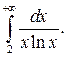 308.
308. 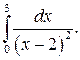
309. 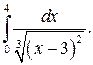 310.
310. 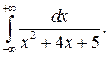
311. Вычислить площадь фигуры, ограниченной параболами 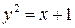 и
и 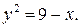
312. Вычислить площадь фигуры, ограниченной гиперболой 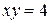 и прямой
и прямой 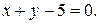
313. Вычислить площадь фигуры, ограниченной астроидой 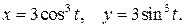
314. Вычислить площадь фигуры, ограниченной кардиоидой 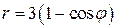 и окружностью
и окружностью 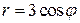 .
.
315. Вычислить объем тела, образованного вращением вокруг оси 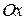 фигуры, ограниченной прямой
фигуры, ограниченной прямой 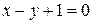 , другой косинусоиды
, другой косинусоиды 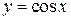 и осью
и осью 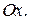
316. Вычислить объем тела, образованного вращением вокруг оси 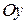 фигуры, ограниченной локоном Аньези
фигуры, ограниченной локоном Аньези 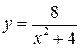 и параболой
и параболой 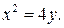
317. Вычислить объем тела, образованного вращением вокруг оси 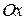 одной арки циклоиды
одной арки циклоиды 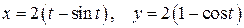 и осью
и осью 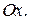
318. Вычислить длину дуги, параболы  от начала координат до точки с абсциссой
от начала координат до точки с абсциссой 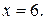
319. Вычислить длину одной арки циклоиды 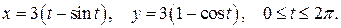
320. Вычислить длину первого витка архимедовой спирали 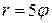 ,
, 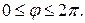
 2015-03-22
2015-03-22 583
583








