Связность в орграфе

Две вершины u и v сильно связаны в орграфе G, если существует маршрут из u в v и из v в u.

Две вершины u и v односторонне связаны в орграфе G, если существует маршрут из u в v, либо из v в u.

Две вершины u и v слабо связаны, если они связаны в графе, который получается из G путем отмены ориентации ребер.

Пример: 2 6

Вершины 1,4,3 – компонента сильной

связанности; 7

Вершина 2 – компонента связанности

Вершины 5, 6, 7 – компонента 1 4 5

сильной связанности

Вершина v орграфа G достижима из вершины u, если

1) v=u;

2) существует маршрут, соединяющий v и u.

Матрицей достижимости орграфа G называется квадратная булевская матрица T(G), у которой

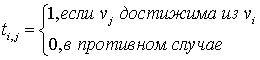
Матрицей контрдостижимости орграфа G называется квадратная булевская матрица Q(G), у которой

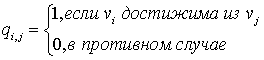
Матрицей сильной связанности орграфа G называется квадратная булевская матрица A(G), у которой

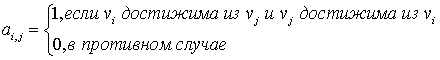
Пример записи матриц для выше представленного графа:

T матрица достижимости

Q – матрица контрдостижимости

А – матрица сильной связанности

Подходящий пример.(Вершины графа обозначить через Y)

Ориентированные графы успешно применяются для схематичного изображения аэролиний, соединяющих города всего мира, или ком­муникационных сетей между компьютерами. В таких сетях важ­но знать последовательность выключений любого соединения (дуги или вершины) по всей сети.

Например, если самолет не может приземлиться для дозаправки в некотором городе вследствие неблагоприятных погодных условий, то ошибка в его переадресации грозит катастрофой: ему может не хватить горючего для достижения неправильно назначенного аэро­порта. Аналогично, если одна или несколько цепей в компьютерной сети не работают, то для некоторых пользователей отдельные серве­ры могут оказаться вообще недоступными.

Таким образом, мы приходим к задаче о поиске путей между произвольной парой вершин в ориентированном графе.

Следующая задача связана с поиском кратчайшего пути, свя­зывающего пару данных вершин в нагруженном орграфе. Слово «кратчайший» здесь вполне уместно, поскольку довольно часто веса в орграфе — это расстояния между пунктами.

Типичная ситуация, которая моделируется нагруженным оргра­фом, это транспортная сеть (по которой товары доставляются из города в город) и коммуникационная сеть (по которой переправля­ется информация).

Рассмотрим нагруженный граф на рис. 8.5. Он может предста­влять, например, длины дорог в милях между шестью деревнями. Поскольку количество вершин в этом графе невелико, то перебрать все возможные пути между любой парой заданных вершин нам впол­не по силам. При этом, естественно, мы найдем наиболее короткий путь, соединяющий соответствующие деревни. В реальной задаче, возникающей в профессиональной деятельности, число вершин, как правило, настолько велико, что такой упрощенный подход к поиску кратчайшего пути слишком неэффективен.

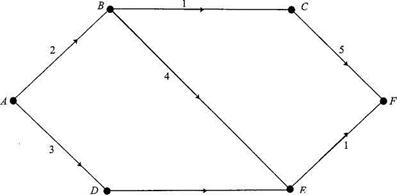
Рисунок 8.5. Нагруженный граф

Существует множество алгоритмов поиска кратчайшего пути.