 Граф – это некоторое конечное множество
Граф – это некоторое конечное множество 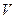 точек, называемых вершинами, и конечный набор
точек, называемых вершинами, и конечный набор 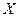 линий, называемых ребрами, соединяющих некоторые пары точек из
линий, называемых ребрами, соединяющих некоторые пары точек из 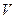 .
.
Пример: схема автомобильных дорог, связывающих города некоторой области, является характерным примером графа.
Ориентированный граф (орграф) – это граф, у которого пары в наборе X являются упорядоченными.
Пример: пусть 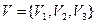 ,
, 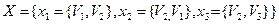 .
.
Тогда 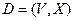 – ориентированный граф.
– ориентированный граф.
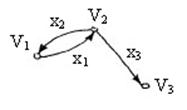
Дуга – это направленное ребро в орграфе.
Пример: в приведенном выше примере для орграфа 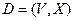 дугами являются ребра
дугами являются ребра 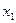 ,
, 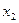 ,
, 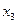 .
.
Начальная вершина – вершина орграфа, которой инцидентны только исходящие дуги.
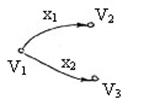
Пример: пусть 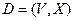 – ориентированный граф,
– ориентированный граф, 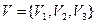 ,
, 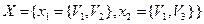 , тогда
, тогда 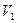 – начальная вершина.
– начальная вершина.
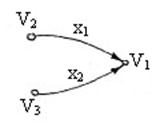 Конечная вершина – вершина орграфа, которой инцидентны только заходящие дуги.
Конечная вершина – вершина орграфа, которой инцидентны только заходящие дуги.
Пример: пусть 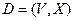 – ориентированный граф,
– ориентированный граф, 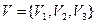 ,
, 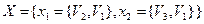 , тогда
, тогда 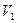 – конечная вершина.
– конечная вершина.
Петля – ребро графа, инцидентное единственной вершине.
Пример: пусть 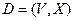 – ориентированный граф,
– ориентированный граф, 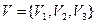 ,
,
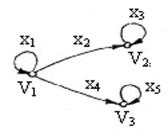
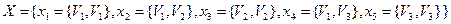 , тогда
, тогда 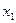 ,
, 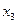 ,
, 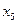 – петли.
– петли.
Изолированная вершина – вершина, которая не имеет инцидентных ребер.
 Пример: пусть
Пример: пусть 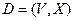 – ориентированный граф,
– ориентированный граф, 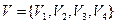 ,
, 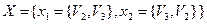 , тогда
, тогда 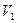 ,
, 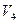 – изолированные вершины.
– изолированные вершины.
Степень вершины – число инцидентных ребер, 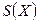 .
.
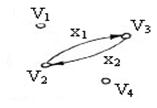
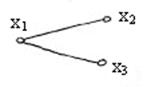
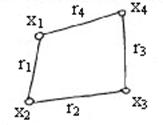
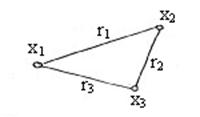
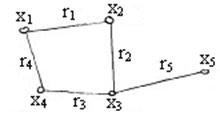
Пример: пусть 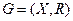 – граф, изображенный на рисунке. Тогда
– граф, изображенный на рисунке. Тогда 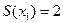 ,
, 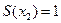 ,
, 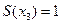 – соответственно степени вершин
– соответственно степени вершин 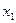 ,
, 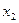 ,
, 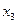 .
.
Псевдограф – граф с кратными ребрами и петлями.
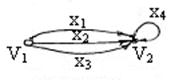
Пример: пусть 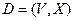 – ориентированный граф,
– ориентированный граф, 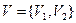 ,
, 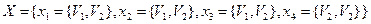 .
.
Тогда 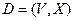 – ориентированный псевдограф.
– ориентированный псевдограф.
Пустой граф – граф 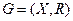 , в котором
, в котором 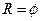 .
.
Пример: пусть 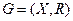 – граф, изображенный на рисунке. Он является пустым, т.к.
– граф, изображенный на рисунке. Он является пустым, т.к. 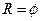 ,
, 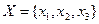

Полный граф – граф 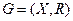 , в котором любая пара вершин инцидентна единственному ребру. Обозначается
, в котором любая пара вершин инцидентна единственному ребру. Обозначается 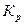 , где
, где 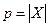 , при этом
, при этом 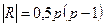 .
.
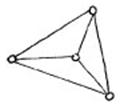
Пример: приведенный на рисунке граф является полным, т.к. это видно из определения и 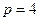 , при этом выполняется
, при этом выполняется 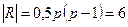 .
.
Мультиграф – граф, в котором имеются кратные (параллельные) ребра.
Мультиграф – это псевдограф без петель.
Пример: пусть 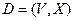 – ориентированный граф,
– ориентированный граф, 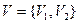 ,
, 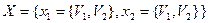 . Тогда
. Тогда 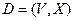 – ориентированный мультиграф.
– ориентированный мультиграф.
Однородный граф – граф, все вершины которого имеют одну и ту же степень.
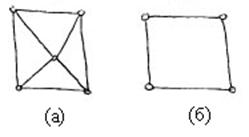
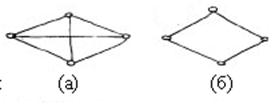
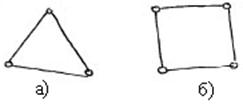 Пример: следующие графы, приведенные на рисунке, являются однородными со степенью вершин
Пример: следующие графы, приведенные на рисунке, являются однородными со степенью вершин 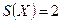 . (рис. (а) и (б))
. (рис. (а) и (б))
Матрица смежности – квадратная матрица 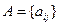 является матрицей смежности графа
является матрицей смежности графа 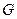 , если при
, если при 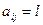 в графе
в графе 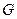 вершины
вершины 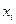 и
и 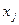 соединены
соединены 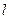 ребрами, при
ребрами, при 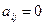 вершины
вершины 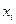 и
и 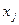 в
в 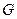 несмежны.
несмежны.
Пример: для орграфа 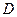 , изображенного на рисунке, приведем матрицу смежности:
, изображенного на рисунке, приведем матрицу смежности:
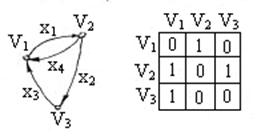
 Матрица инцидентности орграфа
Матрица инцидентности орграфа 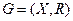 – прямоугольная матрица
– прямоугольная матрица 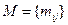 ,
, 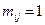 ,если вершина
,если вершина 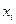 является началом дуги
является началом дуги 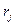 ;
; 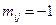 , если вершина
, если вершина 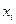 является концом дуги
является концом дуги 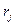 ;
; 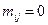 , если вершина
, если вершина 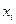 не инцидентна дуге
не инцидентна дуге 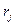 .
.
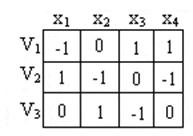
Пример: для орграфа, приведенного в примере для матрицы смежности, составим матрицу инцидентности:
Два графа 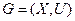 и
и 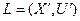 являются изоморфными, если между парами множеств их вершин, ребер и дуг существуют взаимно однозначные соответствия, сохраняющие смежность и ориентацию для дуг.
являются изоморфными, если между парами множеств их вершин, ребер и дуг существуют взаимно однозначные соответствия, сохраняющие смежность и ориентацию для дуг.
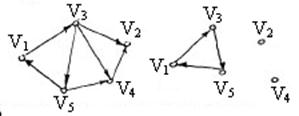
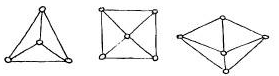 Пример: следующие графы, приведенные на рисунке, изоморфны:
Пример: следующие графы, приведенные на рисунке, изоморфны:
Маршрут длины H – чередующаяся последовательность 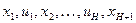 вершин
вершин 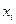 и ребер
и ребер 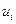 , обладающих тем свойством, что пара соседних элементов инцидентна.
, обладающих тем свойством, что пара соседних элементов инцидентна.
Пример: последовательность 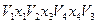 – маршрут длины 3, соединяющий вершины
– маршрут длины 3, соединяющий вершины 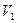 и
и 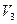 в графе, приведенном на рисунке.
в графе, приведенном на рисунке.
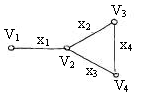
Замкнутый маршрут – маршрут, у которого начальная вершина совпадает с конечной.
Пример: пусть 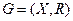 – граф, показанный на рисунке, тогда
– граф, показанный на рисунке, тогда 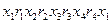 – замкнутый маршрут длины 4.
– замкнутый маршрут длины 4.
Цепь – маршрут, в котором все ребра различны.
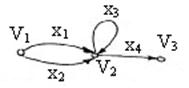
Пример: пусть 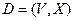 – ориентированный граф, приведенный на рисунке. Тогда
– ориентированный граф, приведенный на рисунке. Тогда 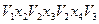 – цепь из
– цепь из 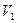 в
в 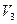 длины 3.
длины 3.
Простая цепь – цепь, в которой все вершины различны.
Пример: для ориентированного графа 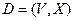 , приведенного выше в примере с цепью,
, приведенного выше в примере с цепью, 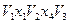 и
и 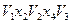 – простые цепи из
– простые цепи из 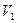 в
в 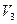 длины 2.
длины 2.
Цикл – цепь, у которой начальная и конечная вершина совпадают.
 Пример: пусть
Пример: пусть 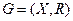 – граф, показанный на рисунке, тогда
– граф, показанный на рисунке, тогда 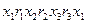 – цикл.
– цикл.
Простой цикл – простая цепь, у которой концевые вершины совпадают.
Пример: пусть 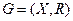 – граф, показанный на рисунке, тогда
– граф, показанный на рисунке, тогда 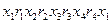 – простой цикл.
– простой цикл.
Эйлеров цикл – это цепь, содержащая все ребра графа в точности один раз, у которой начальная и конечная вершина совпадают.
Пример: пусть  – граф, показанный на рисунке, тогда существует Эйлеров цикл –
– граф, показанный на рисунке, тогда существует Эйлеров цикл – 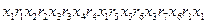 .
.
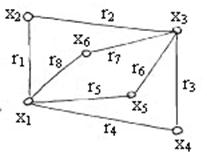
Гамильтонов цикл – это простая цепь, содержащая все вершины графа, у которой начальная и конечная вершины совпадают.
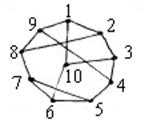 Пример: приведенный на рисунке граф имеет Гамильтонов цикл:
Пример: приведенный на рисунке граф имеет Гамильтонов цикл: 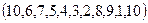 .
.
Путь (ориентированная цепь) – цепь орграфа 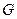 . в которой ориентация дуг (ребер) совпадает.
. в которой ориентация дуг (ребер) совпадает.
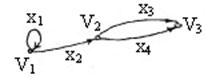
Пример: для ориентированного графа, приведенного на рисунке, имеем путь из 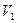 в
в 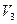 длины 3:
длины 3: 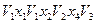 .
.
Простой путь – путь, не содержащий повторяющихся вершин.
Пример: для ориентированного графа, приведенного на рисунке, имеем простой путь из 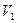 в
в 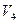 :
: 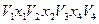 .
.
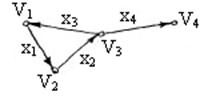
Контур – путь, у которого начальная и конечная вершины совпадают.
Пример: для ориентированного графа, приведенного на рисунке, имеем контур: 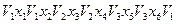
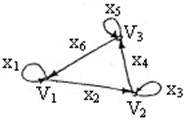
Простой контур – контур, не содержащий повторяющихся вершин.
Пример: для ориентированного графа, изображенного на
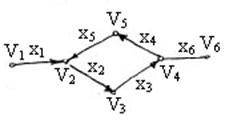
рисунке, имеем простой контур: 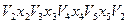 .
.
Подграф графа 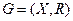 – граф
– граф 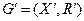 , для которого
, для которого 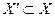 и две вершины в
и две вершины в 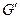 смежны тогда и только тогда, когда они смежны в
смежны тогда и только тогда, когда они смежны в 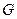 .
.
Пример: пусть 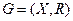 – исходный граф, показанный на рисунке (а), тогда
– исходный граф, показанный на рисунке (а), тогда 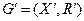 – некоторый подграф графа
– некоторый подграф графа 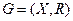 (рисунок (б)).
(рисунок (б)).
Суграф графа 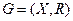 – граф
– граф 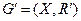 содержит то же множество вершин, что и сам граф
содержит то же множество вершин, что и сам граф 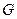 и
и 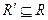 .
.
Пример: пусть 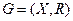 – некоторый исходный граф, показанный на рисунке (а), тогда
– некоторый исходный граф, показанный на рисунке (а), тогда 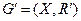 – некоторый суграф графа
– некоторый суграф графа 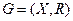 (б).
(б).
Связный граф – граф, у которого любая пара вершин взаимодостижима.
Пример: оба графа, которые были приведены выше в качестве примеров суграфа, являются также связанными графами.
Сильносвязный граф – орграф, у которого любые две вершины взаимодостижимы.
 Пример: следующие два ориентированных графа, показанных на рисунке, являются сильносвязанными орграфами.
Пример: следующие два ориентированных графа, показанных на рисунке, являются сильносвязанными орграфами.
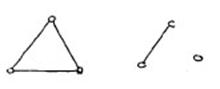
Компонента связности графа – максимальный подграф графа 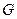 , в котором все вершины попарно достижимы.
, в котором все вершины попарно достижимы.
Пример: у графа, показанного на рисунке, три компоненты связности.
Сильная компонента орграфа 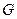 – максимальный подграф орграфа
– максимальный подграф орграфа 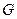 , в котором любая пара вершин сильно связана.
, в котором любая пара вершин сильно связана.
Пример: у орграфа, изображенного на рисунке, три компоненты сильной связности.
Вершина 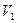 ориентированного графа называется достижимой из вершины
ориентированного графа называется достижимой из вершины 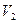 , если существует путь с началом в
, если существует путь с началом в 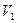 и концом в
и концом в 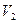 .
.
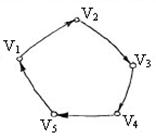 Пример: в приведенном на рисунке орграфе вершина
Пример: в приведенном на рисунке орграфе вершина 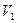 является достижимой из вершины
является достижимой из вершины 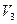 .
.
Минимальная длина простой цепи с началом в 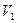 и концом в
и концом в 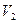 называется расстоянием между этими вершинами.
называется расстоянием между этими вершинами.
Пример: в графе, изображенном на рисунке, расстояние между вершинами 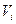 и
и 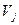 равно трем.
равно трем.
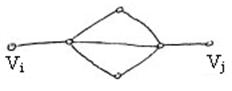
Смешанный граф – это граф, содержащий как дуги, так и ненаправленные ребра.
Пример: граф, показанный на рисунке, является смешанным.
Вершина 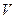 инцидентна дуге
инцидентна дуге 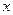 тогда и только тогда, когда
тогда и только тогда, когда 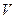 является либо началом, либо концом дуги
является либо началом, либо концом дуги 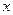 .
.
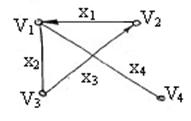
Пример: на рисунке вершины 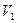 и
и 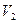 инцидентны дуге
инцидентны дуге 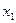 .
.
Отношение смежности:
Две вершины смежны в графе тогда и только тогда, когда существует ребро графа, инцидентное им обоим. Два ребра смежны в графе тогда и только тогда, когда существует, по крайней мере, одна вершина, инцидентная им обоим.
Пример: вершины 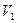 и
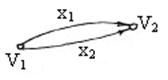
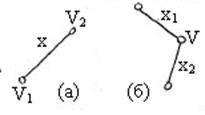
и 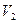 смежны, т.к. существует ребро x, инцидентное им обоим (рис (а)). Ребра
смежны, т.к. существует ребро x, инцидентное им обоим (рис (а)). Ребра 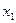 и
и 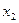 смежны, т.к. существует вершина
смежны, т.к. существует вершина 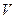 , инцидентная им обоим (рис (б)).
, инцидентная им обоим (рис (б)).
Обыкновенный граф – неориентированный граф, который не содержит параллельных ребер и петель; орграф, который не содержит строго параллельных дуг и петель.
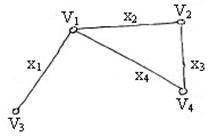
Пример: на рисунке изображен обыкновенный граф  .
.
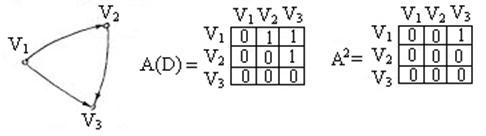
Обозначим через 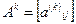 k-ю степень матрицы смежности
k-ю степень матрицы смежности 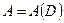 орграфа
орграфа 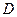 . Тогда элемент
. Тогда элемент 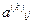 матрицы
матрицы 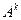 ориентированного псевдографа
ориентированного псевдографа 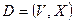 , где
, где 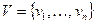 , равен числу всех путей длины
, равен числу всех путей длины 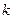 из
из 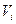 в
в 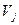 .
.
Пример: существует один путь из 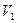 в
в 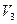 длины 2.
длины 2.
Граф 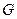 называется деревом, если он является связным и не имеет циклов. Число ребер такого графа равно на единицу меньше числа его вершин.
называется деревом, если он является связным и не имеет циклов. Число ребер такого графа равно на единицу меньше числа его вершин.
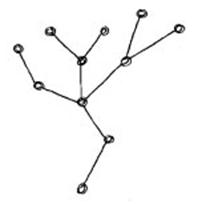
Пример: граф 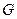 , изображенный на рисунке, является деревом. Из рисунка видно, что выполняется соотношение
, изображенный на рисунке, является деревом. Из рисунка видно, что выполняется соотношение 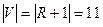 (в нашем случае).
(в нашем случае).
 2015-03-22
2015-03-22 6262
6262







