Множество – состоит из элементов. Принадлежность элемента а множеству М обозначается 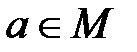 (" а принадлежит М "), не принадлежность –
(" а принадлежит М "), не принадлежность – 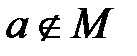 .
.
Множество А называется подмножеством множества В (обозначается 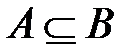 ), если всякий элемент из А является элементом В (рис 1.1). Если множество A является подмножеством множества B и
), если всякий элемент из А является элементом В (рис 1.1). Если множество A является подмножеством множества B и 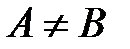 , то А называется строгим подмножеством (обозначается
, то А называется строгим подмножеством (обозначается 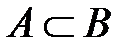 , читается A включено (содержится) в B).
, читается A включено (содержится) в B).
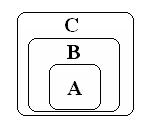
Рисунок 1.1 – Множество С с подмножествами В и А
Содержательные примеры множеств и их возможные обозначения:
N – множество натуральных чисел 1, 2, 3,...;
N 1 – множество натуральных чисел, не превосходящих 100;
R – множество действительных чисел.
Из рис. 2.1 видно, что если 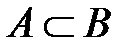 и
и 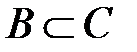 , то
, то 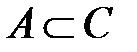 . такое свойство включения называется транзитивностью.
. такое свойство включения называется транзитивностью.
По поводу равенства множеств можно сказать:
Множества А и В равны, если их элементы совпадают (Определение I), или множества А и В равны, если 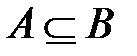 и
и 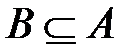 (Определение II).
(Определение II).
Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным (например, множества N, R – бесконечные множества).
Число элементов в конечном множестве А называется его мощностью и обозначается | А |.
Если 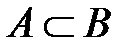 , то | А | < | B |.
, то | А | < | B |.
Множество мощности 0, т.е. не содержащее элементов, называется пустым (обозначается 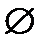 ): |
): | 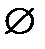 | = 0. Принято считать, что пустое множество является подмножеством любого множества.
| = 0. Принято считать, что пустое множество является подмножеством любого множества.
Множеством подмножеств некоторого произвольного множества U илиего булеаном (обозначается 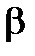 (U)),называется множество, элементами которого являются все подмножества множества U. Оно включает в качестве элементов также пустое множество и само множество U.
(U)),называется множество, элементами которого являются все подмножества множества U. Оно включает в качестве элементов также пустое множество и само множество U.
Мощность булеана равна
| 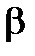 (U)| = 2 n, где n = | U |.
(U)| = 2 n, где n = | U |.
Таким образом, если множество U состоит из n элементов, то его булеан состоит из 2 n элементов.
В конечном множестве можно задать нижнюю и верхнюю границы, обозначаемые
inf A = m и sup A = M,
соответственно. Здесь A – множество, а m и M некоторые элементы множества (не обязательно числа).
Если 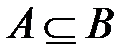 , то inf A
, то inf A  inf B, а sup A
inf B, а sup A 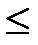 sup B.
sup B.
Приведем способы задания множеств.
Множества можно задавать перечислением, т.е. списком своих элементов. Списком можно задать лишь конечные множества. Обозначение списка – в фигурных скобках. Например, множество А устройств домашнего компьютера, состоящего из процессорного блока a, а также периферийных устройств В (монитора b, клавиатуры с и принтера d), может быть представлено списком:
А = { а, В } или А = { а, b, с, d }.
Необходим внести следующие уточнения:
1) в списке, задающем множество, одинаковые элементы представляются одним элементом (поэтому в множествах нижняя и верхняя границы единственны).
2) перестановка элементов в списке не изменяет множество.
3) задание типа N = 1, 2, 3,... – не список, но лишь допустимое условное обозначение.
Следующий метод задания множества – задание с помощью п орождающей процедурой, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов. В таком случае элементами множества являются все объекты, которые могут быть построены с помощью такой процедуры. Например, множество всех целых чисел, являющихся степенями двойки 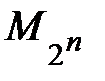 ,
, 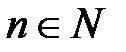 , где N – множество натуральных чисел, (допустимое обозначение
, где N – множество натуральных чисел, (допустимое обозначение 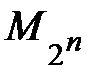 = 1, 2, 4, 8, 16,...) может быть представлено порождающей процедурой, заданной двумя правилами, называемыми рекурсивными:
= 1, 2, 4, 8, 16,...) может быть представлено порождающей процедурой, заданной двумя правилами, называемыми рекурсивными:
1) 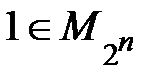 ;
;
2) если 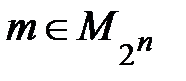 , то
, то 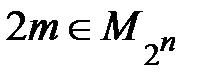 .
.
Последний способ задания множества, этозадание описанием характеристических свойств, которыми должны обладать элементы множества. Обозначается:
М = { х|Р (х)} или М = { х: Р (х)}.
Читается так "Множество М состоит из элементов х таких, что х обладает свойством Р ". Например, множество B периферийных устройств персонального компьютера может быть определено, как B = { х: х – периферийное устройство персонального компьютера}.
Надежным способом точно описать свойство элементов данного множества является задание распознающей процедуры. Она должна устанавливать для любого объекта x, обладает ли он данным свойством Р (и, следовательно, принадлежит множеству) или нет. Например, распознающей процедурой для множества А всех студентов МГУПИ, имеющих студенческие билеты университета, является проверка его наличия. Тогда множество А может быть представлено более точно: " А – множество всех студентов, имеющих студенческие билеты МГУПИ".
Другой пример: для описания характеристического свойства элементов множества 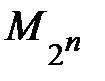 всех целых чисел, являющихся степенями двойки ("быть степенью двойки"), разрешающей процедурой может служить любой метод разложения целых чисел на простые множители.
всех целых чисел, являющихся степенями двойки ("быть степенью двойки"), разрешающей процедурой может служить любой метод разложения целых чисел на простые множители.
Тогда 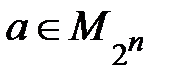 , если а = 1 или если а = 2 х 2 х... х 2 = 2 n,
, если а = 1 или если а = 2 х 2 х... х 2 = 2 n, 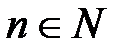 .
.
 2015-03-22
2015-03-22 1254
1254
