Основные законы алгебры множеств (булевой алгебры множеств) представляются в виде тождеств, в которых участвуют символы обозначений множеств, включая символы универсального и пустого множеств, и символы операций объединения, пересечения и дополнения.
Ассоциативный закон:
(X  Y)
Y)  Z = X
Z = X  (Y
(Y  Z) = X
Z) = X  Y
Y  Z
Z
(X  Y)
Y)  Z = X
Z = X  (Y
(Y  Z) = X
Z) = X  Y
Y  Z
Z
X  Y = Y
Y = Y  X
X
X  Y = Y
Y = Y  X
X
Закон идемпотентности (повторения):
X  X = X
X = X
X  X = X
X = X
Дистрибутивный закон:
(X  Y)
Y)  Z = (X
Z = (X  Z)
Z)  (Y
(Y  Z)
Z)
(X  Y)
Y)  Z = (X
Z = (X  Z)
Z)  (Y
(Y  Z)
Z)
Законы универсального U и пустого 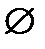 множеств (законы нуля и единицы
множеств (законы нуля и единицы 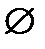
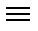 0, U
0, U 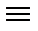 1):
1):
X 
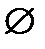 = X
= X
X 
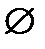 =
= 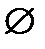
X  U = U
U = U
X  U = X
U = X
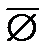 = U
= U
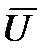 =
= 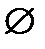 .
.
Законы исключенного третьего и противоречия:
X 
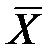 = U
= U
X 
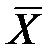 =
= 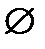
Законы де Моргана:
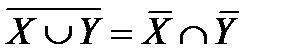
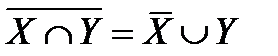
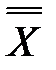 = X.
= X.
При работе с множествами могут оказаться полезными тождества, приведенные ниже. Однако они требуют доказательства. Доказать их можно, используя основные законы.
Дистрибутивный закон пересечения относительно разности:

Дистрибутивный закон пересечения относительно симметрической разности:
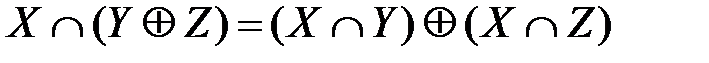
Дистрибутивный закон разности относительно пересечения:
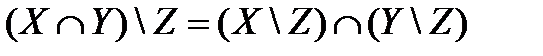
Дистрибутивный закон разности относительно объединения:
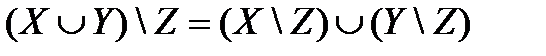
Дистрибутивные законы объединения и пересечения относительно разности:
X \(Y  Z) = (X \ Y)
Z) = (X \ Y)  (X \ Z)
(X \ Z)
X \(Y  Z) = (X \ Y)
Z) = (X \ Y)  (X \ Z)
(X \ Z)
Представление пересечения и объединения через разность:
X  Z = X \(X \ Z)
Z = X \(X \ Z)
X  Y = (X \ Y)
Y = (X \ Y)  (Y \ X)
(Y \ X)  (X
(X  Y) = (X \ Y)
Y) = (X \ Y)  (Y \ X)
(Y \ X)  X \(X \Y)
X \(X \Y)
Законы нуля и единицы для разности:
(X \ Y)  (X
(X  Y) =
Y) = 
X \ 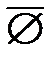 = X \ U =
= X \ U = 
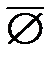 \ X =
\ X = 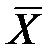
U \ X = 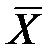
X \ X = U
Законы поглощения:
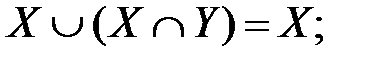
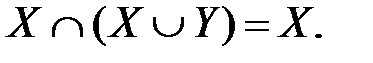
Закон склеивания:
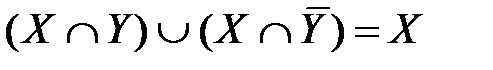
Свойства симметрической разности:
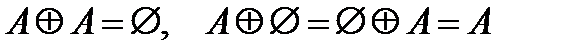 ,
,
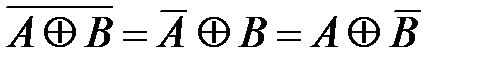 ,
,
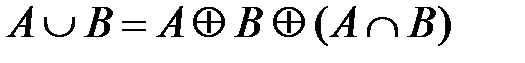 ,
,
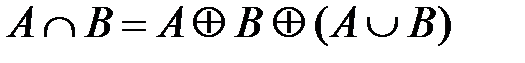 ,
,
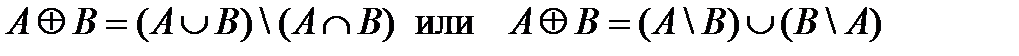 ,
,
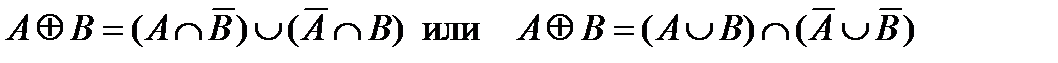 .
.
 2015-03-22
2015-03-22 2417
2417
