Плотность энергетических состояний и распределение электронов по энергиям

Состояние частиц обычно определяют в фазовом пространстве (пространстве импульсов и координат). Электрон, как и другие квантовые частицы с полуцелым спином, подчиняется принципу неопределенности. Это означает, что разным элементам фазового объема будут отвечать различные квантовые состояния лишь в том случае, если объем этих элементов не меньше 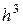, то есть за элементарную ячейку фазового пространства следует принять объем .

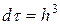Считая потенциальную энергию одинаковой во всех точках физического объема, можно перейти от фазового пространства к пространству импульсов (или 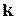- пространству), в котором элементарная ячейка имеет объем 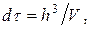где 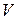– объем кристалла.

Определим плотность энергетических состояний 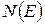, то есть число состояний в единичном интервале энергий для единичного объема кристалла

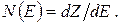(4.70)

Вид функции 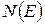зависит от того, как сама энергия выражается через квазиимпульсы частиц. Если в пространстве квазиимпульсов (или 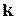-пространстве) через точки с одинаковыми значениями энергии провести поверхность, то получим так называемую изоэнергетическую поверхность.

В приближении свободных электронов энергия определяется выражением

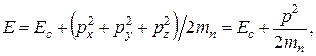(4.71)

где 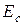– энергия, соответствующая дну зоны проводимости. Изоэнергетическими поверхностями в этом случае являются сферы (рис.4.16).

Объем шарового слоя между сферами радиусов 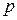и 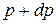равняется 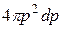. В нем может разместиться элементарных ячеек (с учетом спина электрона) 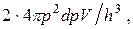а в единичном объеме кристалла

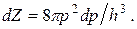(4.72)

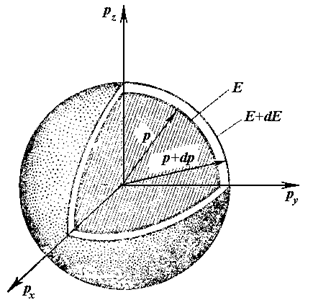Рис.4.16. Изоэнергетические поверхности в пространстве квазиимпульсов

Выражая 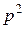и 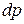из (4.71) и подставляя в (4.72), получаем для плотности состояний в зоне проводимости

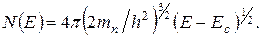(4.73)

Для состояний вблизи потолка валентной зоны энергия имеет вид

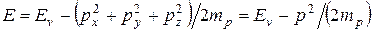(4.74)

и плотность состояний определяется выражением

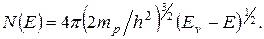(4.75)

Умножив (4.73) на вероятность заполнения данного энергетического состояния электроном, то есть на функцию Ферми-Дирака 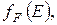получим распределение электронов по энергиям (принимаем )

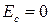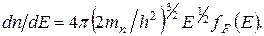(4.76)

С математической точки зрения 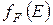есть функция, которая зависит от двух параметров 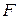и :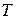

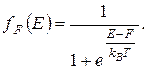(4.77)

Здесь 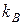есть постоянная Больцмана.

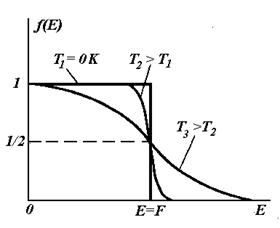
При данной величине энергии Ферми 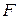функция представляет собой семейство кривых, зависящих от температуры 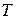(рис.4.17, а). При 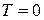функция 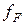терпит разрыв в точке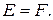

а	б
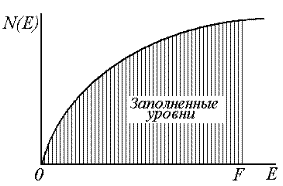
Рис.4.17. Вид функции Ферми при различных температурах (а) и распределение электронов по энергиям (б)

График распределения электронов по энергиям представлен на рис. 4.17, б. При абсолютном нуле температуры состояния в зоне проводимости заполнены вплоть до уровня Ферми, состояния выше энергии Ферми – свободные. При 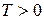часть электронов за счет термического возбуждения переходит на свободные уровни, лежащие выше уровня Ферми.