В нашей задаче имеется три этапа, на каждом из которых мы должны принять решение о реконструкции первого, второго и третьего предприятия соответственно. Состояние системы  на каждом этапе
на каждом этапе 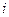 ,
,  , описывается наличием неизрасходованных денежных средств. Поскольку с самого начала у нас имеется 39 млн. рублей, и мы должны расходовать целое число миллионов, можно считать, что на каждом шаге количество неизрасходованных денег
, описывается наличием неизрасходованных денежных средств. Поскольку с самого начала у нас имеется 39 млн. рублей, и мы должны расходовать целое число миллионов, можно считать, что на каждом шаге количество неизрасходованных денег  есть целое число от 0 до 39.
есть целое число от 0 до 39.
Выпишем функцию 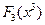 . Если к моменту принятия решения о реконструкции третьего предприятия известно, сколько осталось денег, то оптимальное решение очень простое ¾ мы проводим самую дорогую реконструкцию, какая нам доступна. Результат оформим в виде таблицы.
. Если к моменту принятия решения о реконструкции третьего предприятия известно, сколько осталось денег, то оптимальное решение очень простое ¾ мы проводим самую дорогую реконструкцию, какая нам доступна. Результат оформим в виде таблицы.
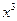 | 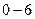 | 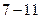 | 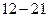 | 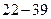 |
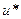 | ||||
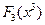 |
Теперь рассмотрим второе предприятие и вычислим функцию 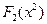 .
.
Пусть сначала 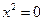 . Тогда имеется единственная возможность
. Тогда имеется единственная возможность 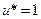 ,
, 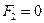 . Если
. Если 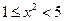 , то имеется два доступных проекта по второму предприятию: проекты №1 и №2. При этом на реконструкцию третьего предприятия остается денег
, то имеется два доступных проекта по второму предприятию: проекты №1 и №2. При этом на реконструкцию третьего предприятия остается денег 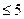 , поэтому прибыль последующих этапов равна 0. Имеем:
, поэтому прибыль последующих этапов равна 0. Имеем:
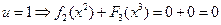 ,
,
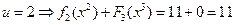 .
.
Следовательно, при 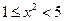
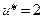 ,
, 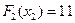 . Если
. Если 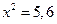 , имеется три возможности:
, имеется три возможности:
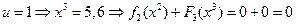 ,
,
 ,
,
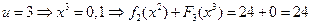 .
.
Максимум из этих трех выражений достигается в третьей строке, следовательно, 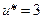 ,
, 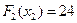 . Если
. Если 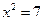 , то имеются следующие три возможности:
, то имеются следующие три возможности:
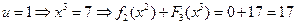 ,
,
 ,
,
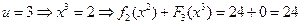 .
.
Максимум из этих трех выражений достигается в третьей строке, следовательно, 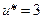 ,
, 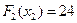 . Если
. Если 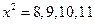 , то:
, то:
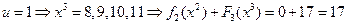 ,
,
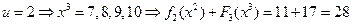 ,
,
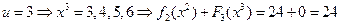 .
.
Максимум достигается во второй строке, следовательно, 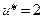 ,
, 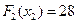 . Если
. Если 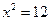 , то все четыре проекта реконструкции на втором этапе становятся доступны.
, то все четыре проекта реконструкции на втором этапе становятся доступны.
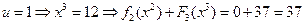 ,
,
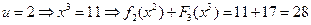 ,
,
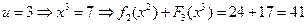 ,
,
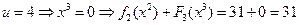 .
.
Максимум достигается в третьей строке, следовательно, 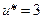 ,
, 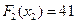 . Если
. Если 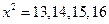 , то имеем:
, то имеем:
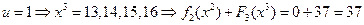 ,
,
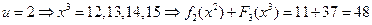 ,
,
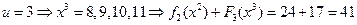 ,
,
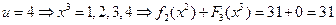 .
.
Максимум достигается во второй строке, следовательно, 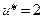 ,
, 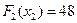 . Если
. Если 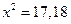 , то имеем:
, то имеем:
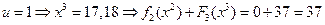 ,
,
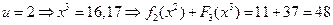 ,
,
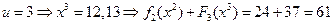 ,
,
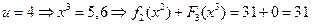 .
.
Максимум достигается в третьей строке, следовательно, 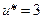 ,
, 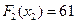 . Если
. Если 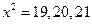 , то имеем:
, то имеем:
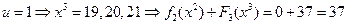 ,
,
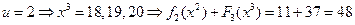 ,
,
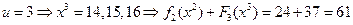 ,
,
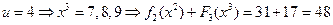 .
.
Максимум достигается в третьей строке, следовательно, 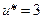 ,
, 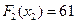 . Если
. Если 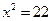 , то тогда:
, то тогда:
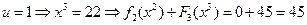 ,
,
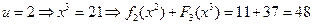 ,
,
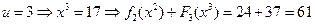 ,
,
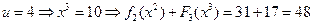 .
.
Максимум, по-прежнему, достигается в третьей строке, следовательно, 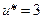 ,
, 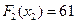 . Если
. Если 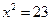 , то тогда:
, то тогда:
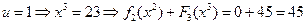 ,
,
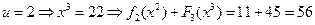 ,
,
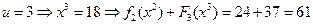 ,
,
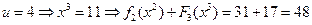 .
.
Максимум достигается в третьей строке, следовательно, 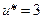 ,
, 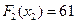 . При
. При 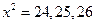 , имеем:
, имеем:
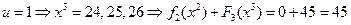 ,
,
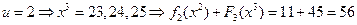 ,
,
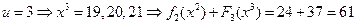 ,
,
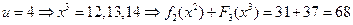 .
.
Максимум достигается во второй строке, следовательно, 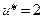 ,
, 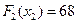 . Если
. Если 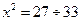 , то тогда:
, то тогда:
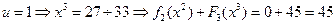 ,
,
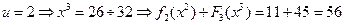 ,
,
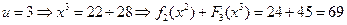 ,
,
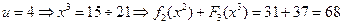 .
.
Максимум достигается в третьей строке, следовательно, 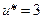 ,
, 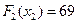 . Наконец, при
. Наконец, при 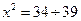 , то тогда:
, то тогда:
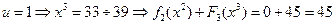 ,
,
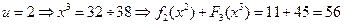 ,
,
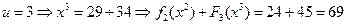 ,
,
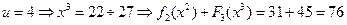 .
.
Максимум достигается в четвертой строке, следовательно, 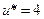 ,
, 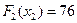 . Оформим полученные результаты в виде таблицы.
. Оформим полученные результаты в виде таблицы.
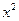 | 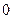 | 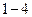 | 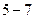 | 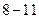 | |
 | |||||
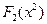 |
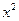 | 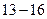 | 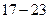 | 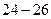 | 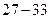 | 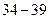 |
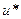 | |||||
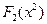 |
Остается рассмотреть первый этап. Начальное состояиние здесь ровно одно, 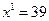 . Посмотрим, какую суммарную прибыль мы получим, если примем каждой из четырех возможных решений о реконструкции первого предприятия. Получаем:
. Посмотрим, какую суммарную прибыль мы получим, если примем каждой из четырех возможных решений о реконструкции первого предприятия. Получаем:
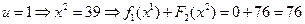 ,
,
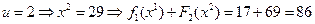 ,
,
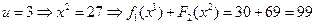 ,
,
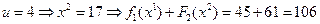 .
.
Максимум достигается в четвертой строке, следовательно, 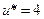 ,
, 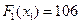 . Теперь мы можем восстановить цепочку оптимальных решений по реконструкции всех трех предприятий. Первое предприятие мы реконструируем по проекту №4. При этом затрачиваем 22 млн. рублей, получая 45 млн. рублей чистой прибыли. К моменту принятия решения о втором предприятии нам остается распределить 39-22=17 млн. рублей, поэтому оптимальным является решение №3 (эта информация имеется в таблице, задающей функцию
. Теперь мы можем восстановить цепочку оптимальных решений по реконструкции всех трех предприятий. Первое предприятие мы реконструируем по проекту №4. При этом затрачиваем 22 млн. рублей, получая 45 млн. рублей чистой прибыли. К моменту принятия решения о втором предприятии нам остается распределить 39-22=17 млн. рублей, поэтому оптимальным является решение №3 (эта информация имеется в таблице, задающей функцию 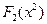 ). При этом мы затрачиваем 5 млн. рублей, получаем чистой прибыли 24 млн. рублей, и сохраняем 17-5=12 млн. рублей для реконструкции третьего предприятия. С этой суммой для реконструкции третьего предприятия мы выбираем проект №3, затрачивая 12 млн. рублей и получая чистой прибыли 37 млн. рублей. Суммарная прибыль 45+24+37=106 млн. рублей.
). При этом мы затрачиваем 5 млн. рублей, получаем чистой прибыли 24 млн. рублей, и сохраняем 17-5=12 млн. рублей для реконструкции третьего предприятия. С этой суммой для реконструкции третьего предприятия мы выбираем проект №3, затрачивая 12 млн. рублей и получая чистой прибыли 37 млн. рублей. Суммарная прибыль 45+24+37=106 млн. рублей.
 2015-03-22
2015-03-22 1008
1008








