В этом разделе математического анализа рассматриваются гладкие конечномерные задачи на экстремум с ограничениями типа равенства и неравенства. Необходимое условие экстремума в таких задачах ¾ принцип Лагранжа снятия ограничений, формулировку которого мы сейчас приведем. Этот метод позволяет свести решение задачи с ограничениями типа равенства и неравенства к решению некоторой системы алгебраических уравнений.
Пусть имеется некоторый набор гладких функций f 0(x), f 1(x), …, fk (x), 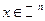 . Рассмотрим следующую задачу на условный экстремум:
. Рассмотрим следующую задачу на условный экстремум:
f 0(x)®min, f 1(x)=0, …, fm (x)=0, fm +1(x)£0, …, fk (x)£0.
Предположим, что x 0 является точкой локального минимума задачи. Тогда существует такой набор чисел (l 0, l 1, …, lm , lm +1, …, lk) (не равных нулю одновременно), называемых множителями Лагранжа, что для функции Лагранжа
L (x, l 0, l 1,…, lm , lm +1,…, lk)= l 0 f 0(x)+ l 1 f 1(x)+…
+ lmfm (x)+ lm +1 fm +1(x)+…+ lkfk (x)
выполнены следующие три условия:
1) условие стационарности по x (теорема Ферма):
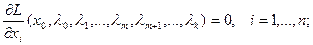
условие неотрицательности:
l 0³0, lm +1³0, …, lk ³0;
условие дополняющей нежесткости:
lm +1 fm +1(x 0)=0, …, lkfk (x 0)=0.
Для задач, в которых минимизируемый функционал и множество допустимых точек являются выпуклыми, необходимые условия минимума являются одновременно и достаточными условиями минимума. Кроме того, если выполнено так называемое условие Слейтера, то есть множество допустимых точек не пусто, то в условиях теоремы Лагранжа можно положить 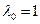 .
.
Покажем, как с помощью теоремы Лагранжа можно находить точки экстремума в простейших конечномерных задачах.
Задача 7.3. Используя правило множителей Лагранжа, решить следующую задачу квадратичного программирования:
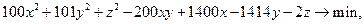
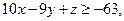
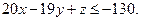
Решение. Выпишем функцию Лагранжа
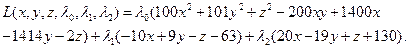
Поскольку задача выпуклая, можно считать, что 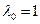 . Условия стационарности запишутся в виде
. Условия стационарности запишутся в виде
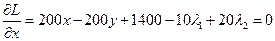 ,
,
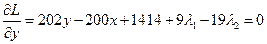 ,
,
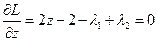 .
.
Условия дополняющей нежесткости имеют вид
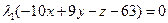 ,
,
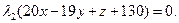
Наконец, условия неотрицательности имеют вид
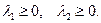
В результате получаем пять соотношений типа равенства на пять неизвестных  ,
,  ,
,  ,
, 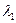 ,
, 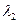 и 4 соотношения типа неравенства.
и 4 соотношения типа неравенства.
Разрешая условия стационарности относительно 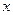 ,
,  ,
, 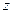 , получим
, получим
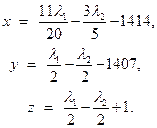
Проанализируем условия дополняющей нежесткости. Всего имеется 4 различных возможности:
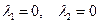 ,
,
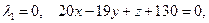
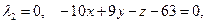
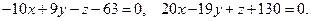
В первом случае получаем:
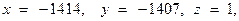
что не удовлетворяет условию 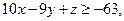 поскольку
поскольку 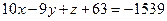 .
.
Во втором случае получаем
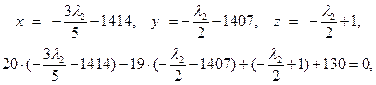
откуда
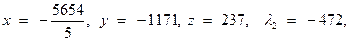
что не удовлетворяет условию неотрицательности множителя 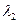 .
.
В третьем случае получаем:
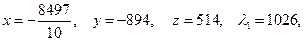
что не удовлетворяет неравенству 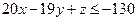 , поскольку в этом случае
, поскольку в этом случае 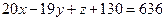 .
.
Наконец, в четвертом, последнем случае получаем:
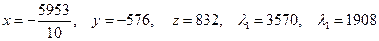 ,
,
что удовлетворяет всем условиям теоремы Лагранжа. Следовательно, точка 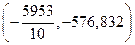 является решением исходной задачи.
является решением исходной задачи.
Методы нелинейного программирования нам потребуются для решения следующей задачи финансовой математики.
Задача 7.4. На фондовом рынке имеются акции трех видов. Доходность по каждой из них является случайной величиной со следующими характеристиками. Первая бумага имеет постоянную доходность m 0 = 10. У второй и третьей бумаги известны средние показатели доходности, равные m 1 = 17 и m 2 = 27 соответственно, и ковариационная матрица 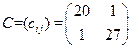 Требуется сформировать портфель (x 0 ,x 1 ,x 2) минимального риска, то есть распределить денежные средства в сумме 1 у.е. между этими тремя бумагами (x 0 +x 1 +x 2 = 1), так чтобы
Требуется сформировать портфель (x 0 ,x 1 ,x 2) минимального риска, то есть распределить денежные средства в сумме 1 у.е. между этими тремя бумагами (x 0 +x 1 +x 2 = 1), так чтобы
1) получить среднюю ожидаемую доходность m 0 x 0 +m 1 x 1 +m 2 x 2 не меньше, чем 18;
2) обеспечить минимальный риск вложения c 11 x 12 + 2 c 12 x 1 x 2 + c 22 x 22 (дисперсию случайной величины доходности).
Для решения использовать правило множителей Лагранжа.
Решение. Запишем задачу в математической форме:
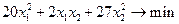 ,
,
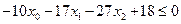 ,
,
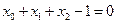 ,
,
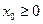 ,
, 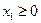 ,
, 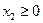 .
.
Поскольку дисперсия любого вложения есть неотрицательная функция, функционал в нашей задаче выпуклый, а линейные ограничения выделяют выпуклое множество в пространстве с координатами 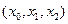 . Отсюда следуют два вывода. Во-первых, необходимые условия минимума являются одновременно и достаточными (то есть любой набор
. Отсюда следуют два вывода. Во-первых, необходимые условия минимума являются одновременно и достаточными (то есть любой набор 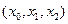 , удовлетворяющий условиям теоремы Лагранжа, является оптимальным). Во-вторых, так как выполнено условие Слейтера, можно считать, что
, удовлетворяющий условиям теоремы Лагранжа, является оптимальным). Во-вторых, так как выполнено условие Слейтера, можно считать, что 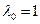 . Составим функцию Лагранжа:
. Составим функцию Лагранжа:
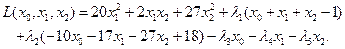
Условия стационарности имеют вид
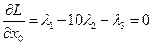 ,
,
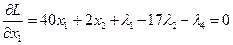 ,
,
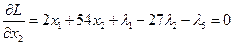 .
.
Условия дополняющей нежесткости имеют вид:
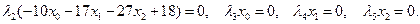 Условия неотрицательности имеют вид:
Условия неотрицательности имеют вид:
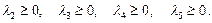
Разрешим систему уравнений

относительно 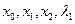 :
:
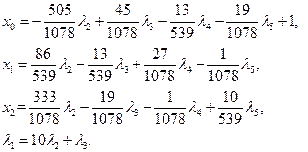
Учтем условия дополняющей нежесткости. В принципе, может наблюдаться 16 различных комбинаций этих условий.
1) 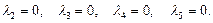
2) 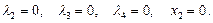
3) 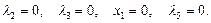
4) 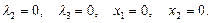
5) 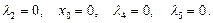
6) 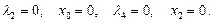
7) 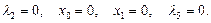
8) 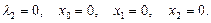
9) 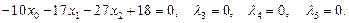
10) 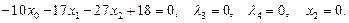
11) 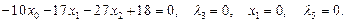
12) 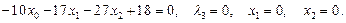
13) 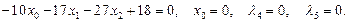
14) 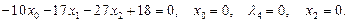
15) 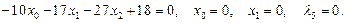
16) 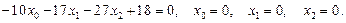
Наша задача заключается в последовательном анализе этих условий.
1) Подставляя значения 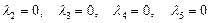 в соотношения
в соотношения
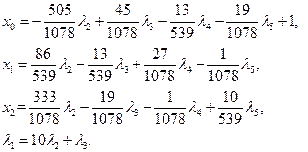
получим
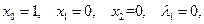
откуда следует, что математическое ожидание доходности портфеля равно 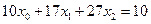 и не удовлетворяет ограничению
и не удовлетворяет ограничению 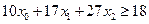 .
.
2) Если 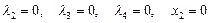 , то
, то
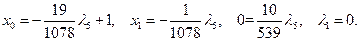
Отсюда вновь 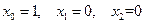 , что, как мы видели, не возможно.
, что, как мы видели, не возможно.
3) Если 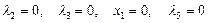 , то
, то
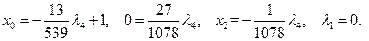
Отсюда вновь следует, что 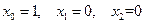 .
.
4) Если 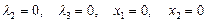 , то
, то
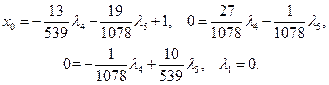
Разрешая уравнения
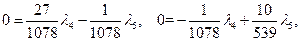
относительно 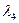 ,
, 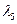 получим
получим 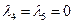 , откуда
, откуда 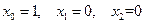 .
.
5) Пусть 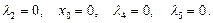 Тогда
Тогда
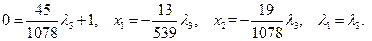
Из первого уравнения следует, что 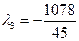 противоречит условию неотрицательности
противоречит условию неотрицательности 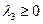 .
.
6) Пусть 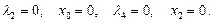 Тогда
Тогда
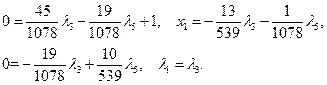
Разрешая уравнения 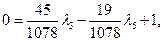
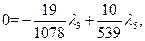 относительно,
относительно, 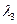 ,
, 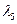 , получим
, получим 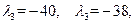 что также противоречит условию неотрицательности.
что также противоречит условию неотрицательности.
7) Пусть 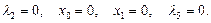 Тогда
Тогда
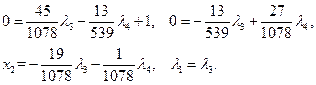
Из первых двух уравнений следует, что 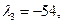
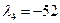 , что вновь не удовлетворяет условию неотрицательности.
, что вновь не удовлетворяет условию неотрицательности.
8) Случай 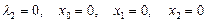 невозможен, поскольку
невозможен, поскольку 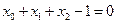 .
.
9) Рассмотрим случай
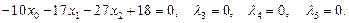
Получаем:
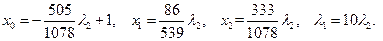
Подставляя  ,
, 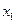 ,
, 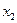 в уравнение
в уравнение
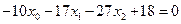 ,
,
получаем
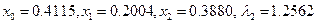 .
.
Поскольку все ограничения типа равенства и неравенства принципа Лагранжа соблюдены, мы нашли оптимальное распределение средств между ценными бумагами.
Остальные 7 случаев рассматривать уже нет необходимости. Ответ: 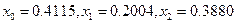 .
.
 2015-03-22
2015-03-22 835
835








