Все уравнения теории упругости значительно упрощаются, если решение задачи сводится к отысканию функции только двух переменных х и у.
В упругом теле возникает плоская деформация, если все перемещения будут происходить только параллельно плоскости хОу
u=u(x,y) v=v(x,y) w=0
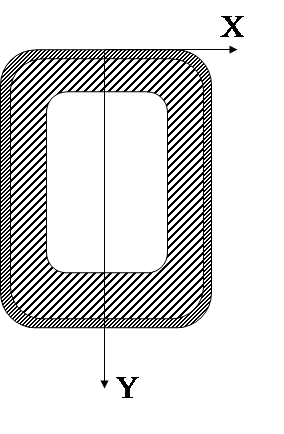
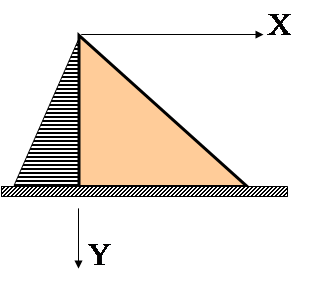
Можно считать. что плоская деформация имеет место в длиной подпорной стенке или плотине, тоннеле метрополитена.
Из формул Коши следует:
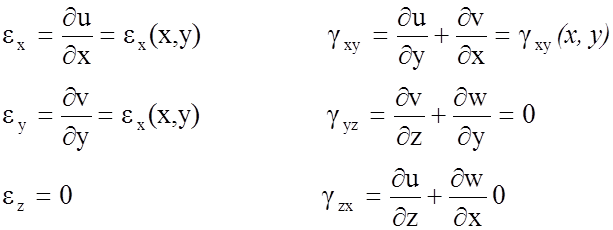
Напряжения σz ≠0
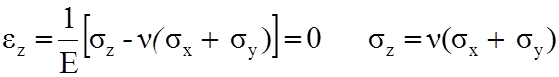
Подставим эти выражения в формулы закона Гука.
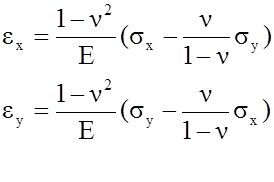
Из полученных формул следует
τyz = τzy =0 σx = σx (x,y) σy = σy (x,y) τxy = τyx(x,y)
σz = σz (x,y)
Основные уравнения теории упругости упрощаются.
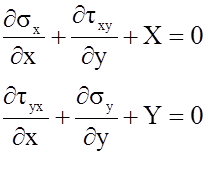
Условия на поверхности
Xν = σx l + τxуm
Yν = τуz l + σy m
2. Уравнения Коши
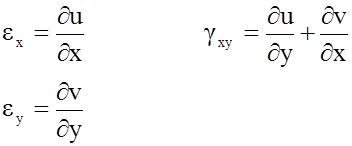
3.Уравнния сплошности
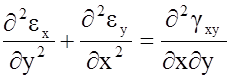
4. Формулы закона Гука
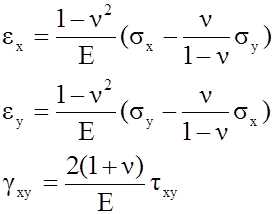
Для упрощения выражений вводятся новые упругие постоянные
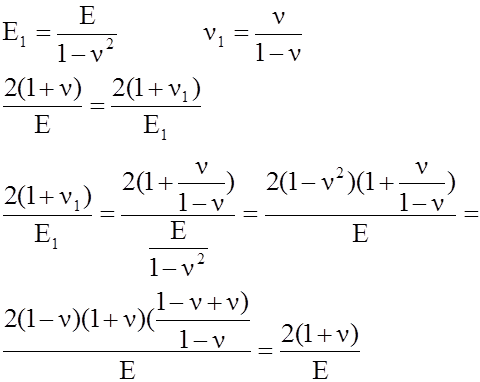
Таким образом формулы закона Гука для случая плоской деформации имеют вид
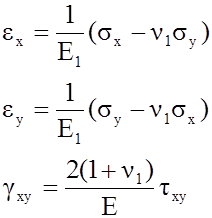
 |
 2015-03-27
2015-03-27 1637
1637








