1. Поле бесконечной равномерно заряженной плоскости
Величину заряда, приходящуюся на единицу поверхности, называют поверхностной плотностью s:
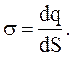 (3.30)
(3.30)
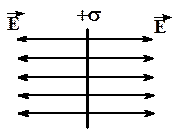 Рис.3.11 Рис.3.11 | Пусть плоскость заряжена положительно с поверхностной плотностью заряда +s=const. Из соображений симметрии силовые линии имеют вид прямых, перпендикулярных плоскости и выходящих из положительных зарядов (рис.3.11). |
Найдем напряженность в точке A (рис.3.12).
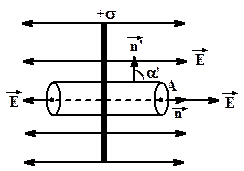 Рис.3.12 Рис.3.12 | В соответствии с законом Кулона для нахождения величины 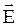 в т. A нужно плоскость разделить на точечные заряды и потом суммировать величины в т. A нужно плоскость разделить на точечные заряды и потом суммировать величины 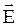 , созданные каждым из этих зарядов. Эта процедура довольно сложная. Теорема Гаусса позволяет решить задачу по отысканию , созданные каждым из этих зарядов. Эта процедура довольно сложная. Теорема Гаусса позволяет решить задачу по отысканию 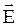 очень просто. Через т. A нужно провести замкнутую поверхность и найти поток очень просто. Через т. A нужно провести замкнутую поверхность и найти поток 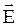 через нее. через нее. |
Поверхность обычно берут такой, чтобы максимально просто можно было бы вычислить ее площадь. В случае заряженной плоскости этой поверхностью является цилиндрическая, у которой образующая перпендикулярна плоскости. Поскольку линии 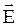 перпендикулярны заряженной плоскости и угол aмежду вектором
перпендикулярны заряженной плоскости и угол aмежду вектором 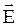 и нормалью к основаниям цилиндра равен нулю, следовательно, cosa=1. Для боковой же поверхности
и нормалью к основаниям цилиндра равен нулю, следовательно, cosa=1. Для боковой же поверхности 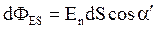 . Угол a’=90°, следовательно, cosa=0 и
. Угол a’=90°, следовательно, cosa=0 и 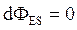 .
.
Итак, общий поток вектора 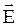 через замкнутую цилиндрическую поверхность
через замкнутую цилиндрическую поверхность 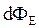 равен сумме потоков через два основания
равен сумме потоков через два основания 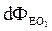 и
и 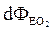 и потоку через боковую поверхность
и потоку через боковую поверхность 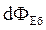 :
:
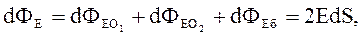 (3.31) где
(3.31) где 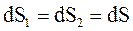 - берем элементарные площадки одинаковой величины.
- берем элементарные площадки одинаковой величины.
Суммарный заряд внутри цилиндра 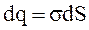 . Тогда по теореме Гаусса запишем:
. Тогда по теореме Гаусса запишем:
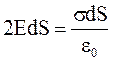
и получаем:
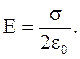 (3.32)
(3.32)
Найдем разность потенциалов поля между точками 1 и 2 на расстоянии x1 и x2 от плоскости:
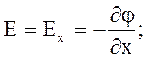
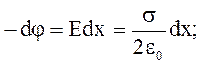
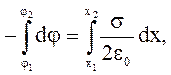
откуда получим:
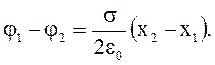 (3.33)
(3.33)
2. Поле бесконечной нити, заряженной с линейной плотностью l
Линейная плотность заряда – заряд, приходящийся на единицу длины:
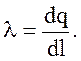 (3.34)
(3.34)
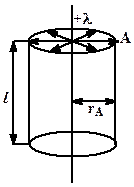 Рис.3.13 Рис.3.13 | Для нахождения 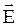 в т. Aудобно выбрать замкнутую поверхность в виде цилиндра (рис.3.13). Линии в т. Aудобно выбрать замкнутую поверхность в виде цилиндра (рис.3.13). Линии 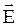 перпендикулярны нити, следовательно, поток вектора перпендикулярны нити, следовательно, поток вектора 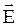 будет только через боковую поверхность цилиндра. Тогда будет только через боковую поверхность цилиндра. Тогда 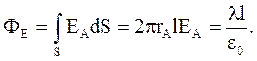 Следовательно, Следовательно, 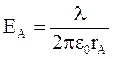 . (3.35) . (3.35) |
Разность потенциалов между точками 1 и 2 поля, лежащими на расстоянии r1 и r2 от оси цилиндра:
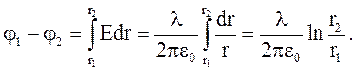 (3.36)
(3.36)
3. Поле заряженной сферической поверхности
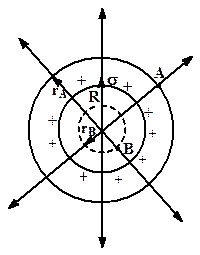 Рис.3.14 Рис.3.14 | Проводим вокруг полой металлической сферы сферическую поверхность радиусом rA (рис.3.14). Поток вектора через эту поверхность 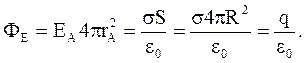 Тогда Тогда 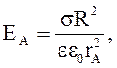 или или 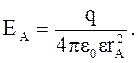 (3.37) (3.37) |
Из (3.37) видно, что выражение для 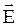 получилось таким же, как и для точечного заряда.
получилось таким же, как и для точечного заряда.
Внутри сферы, например в т.B, величина 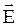 =0, т.к заряд внутри сферы, проведенной через т. B, равен нулю. Величина
=0, т.к заряд внутри сферы, проведенной через т. B, равен нулю. Величина 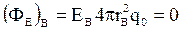 и
и 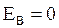 .
.
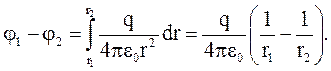 (3.38)
(3.38)
Шар, представляющий собой диэлектрик, может быть внутри равномерно заряжен с объемной плотностью 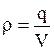 . Поток вектора
. Поток вектора 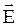 через поверхность радиусом r<R (R – радиус шара) равен
через поверхность радиусом r<R (R – радиус шара) равен 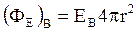 . Заряд внутри сферы радиусом r равен:
. Заряд внутри сферы радиусом r равен: 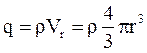 .
.
По теореме Гаусса
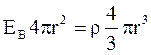 и
и 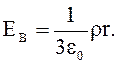 (3.39)
(3.39)
За пределами равномерно заряженного шара выражение для EA будет таким же, как и полученное нами для полой сферы 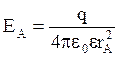 , только величина q будет равняться rV:
, только величина q будет равняться rV:
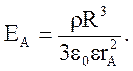 (3.40)
(3.40)
Разность потенциалов для точек, лежащих на расстоянии r>R от центра шара:
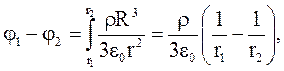 (3.41)
(3.41)
и для точек, лежащих на расстоянии r<R от центра шара:
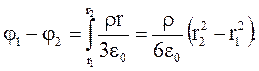 (3.42)
(3.42)
 2015-03-27
2015-03-27 3401
3401








