Пусть f определена на множестве Х. Если существует 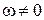 такое, что
такое, что 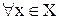 числа
числа 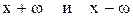 также принадлежат множеству Х и
также принадлежат множеству Х и 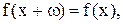
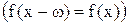 , то функцию f называют периодической с периодом
, то функцию f называют периодической с периодом 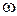 .
.
Примеры:
1) 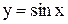 периодическая с периодом
периодическая с периодом 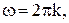 где
где 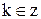 ;
;
2) 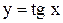 периодическая с периодом
периодическая с периодом 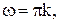 где
где 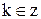 ;
;
3) дробная часть числа: 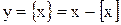 - периодическая,
- периодическая, 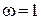 .
.
Установление факта периодичности функции существенно облегчает ее изучение и построение графика: периодическую функцию можно исследовать в пределах одного периода. Для построения графика периодической функции с периодом 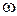 достаточно построить график этой функции на интервале
достаточно построить график этой функции на интервале 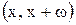 , а затем полученный график периодически продолжить. Рассмотрим некоторые примеры на установление периодичности функции.
, а затем полученный график периодически продолжить. Рассмотрим некоторые примеры на установление периодичности функции.
Пример. 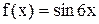
Существует ли такое 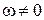 , чтобы для всех действительных х выполнялосьусловие
, чтобы для всех действительных х выполнялосьусловие 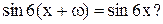
Имеем 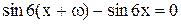 ,
, 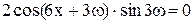 , это выполняется при
, это выполняется при 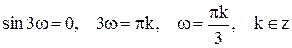 . Следовательно, такие
. Следовательно, такие 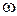 существуют, функция является периодической, наименьший ее положительный период
существуют, функция является периодической, наименьший ее положительный период 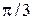 .
.
Пример 2. 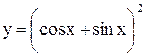 .
.
Имеем 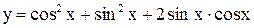 или
или 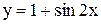 - периодическая функция с периодом
- периодическая функция с периодом 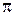 .
.
 2015-03-27
2015-03-27 500
500








