Функция f, определенная на множестве Х, называется ограниченной на множестве 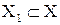 , если множество ее значений f(x) на множестве
, если множество ее значений f(x) на множестве 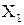 ограничено, т.е. существуют постоянные m и М такие, что
ограничено, т.е. существуют постоянные m и М такие, что 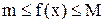 . В противном случае функция называется неограниченной.
. В противном случае функция называется неограниченной.
Примеры:
1) 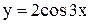 ограничена на всей числовой оси, т.к.
ограничена на всей числовой оси, т.к. 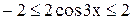 ;
;
2) функция 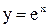 ограничена снизу, так как
ограничена снизу, так как 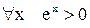 ;
;
3) функция 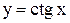 ограничена на промежутке
ограничена на промежутке 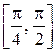 , но ограничена на про-межутке
, но ограничена на про-межутке 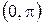 .
.
 2015-03-27
2015-03-27 1804
1804








