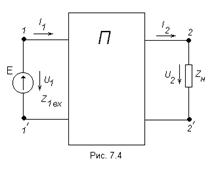
У симметричного четырёхполюсника любую пару выводов ( или
или  ) можно принять за входную, при этом режимы работы источника питания и нагрузки не изменятся. Для определённости предположим, что питание подаётся на зажимы
) можно принять за входную, при этом режимы работы источника питания и нагрузки не изменятся. Для определённости предположим, что питание подаётся на зажимы  (рис. 7.4).
(рис. 7.4).
Найдём входное сопротивление 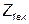 с учетом того, что для симметричного четырёхполюсника
с учетом того, что для симметричного четырёхполюсника 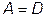
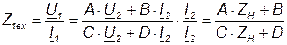 . (7.11)
. (7.11)
На практике очень важное значение имеет правильный выбор сопротивления нагрузки. Например, при подключении телевизионной антенны к телевизору, его сопротивление выбирают так, чтобы входное сопротивление 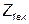 кабеля (по сути четырёхполюсника) на выводах
кабеля (по сути четырёхполюсника) на выводах 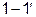 было одинаковым и равным
было одинаковым и равным 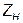 (на выводах
(на выводах 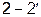 ) независимо от длины кабеля.
) независимо от длины кабеля.
То есть необходимо иметь 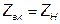 , согласно выражению 7.11 запишем:
, согласно выражению 7.11 запишем:
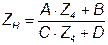 . (7.11а)
. (7.11а)
Решив уравнение 7.11а относительно переменной 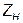 , найдём:
, найдём:
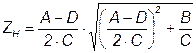
С учетом симметричности четырёхполюсника запишем:
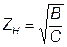 .
.
Полученный параметр 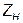 обозначают
обозначают 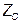 и называют характеристическим сопротивлением.
и называют характеристическим сопротивлением.
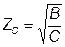 . (7.12)
. (7.12)
Режим четырёхполюсника при 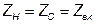 называется режимом согласованной нагрузки.
называется режимом согласованной нагрузки.
В качестве второго параметра симметричного четырёхполюсника выбирают величину, с помощью которой удобно сравнивать напряжения и токи на входе и на выходе четырёхполюсника при согласованной нагрузке.
Рассмотрим схему на рис. 7.4 при согласованной нагрузке.
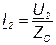
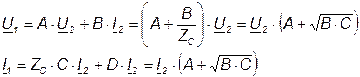
Комплексное число 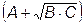 полагают равным
полагают равным 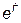 . Где комплексная безразмерная величина
. Где комплексная безразмерная величина 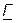 называется постоянной передачи четырехполюсника.
называется постоянной передачи четырехполюсника.
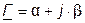 ; (7.13)
; (7.13)
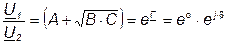 ; (7.14)
; (7.14)
Можно записать:
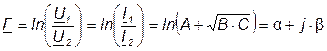 . (7.15)
. (7.15)
Коэффициент 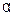 называется постоянной ослабления и является физической безразмерной величиной. Поэтому её единицей измерения служат Неперы (Нп) и Белы (Б).
называется постоянной ослабления и является физической безразмерной величиной. Поэтому её единицей измерения служат Неперы (Нп) и Белы (Б).
Неперы определены на основе натуральных логарифмов:
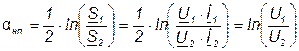 . (7.16)
. (7.16)
Белы получены на основе десятичных логарифмов:
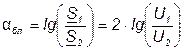 , (7.17)
, (7.17)
в деци Белах:
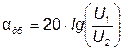 ; (7.18)
; (7.18)
Неперы можно выразить через Белы, и, наоборот, с помощью соотношений:
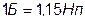
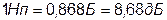
Коэффициент 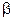 называется постоянной фазы и показывает сдвиг фаз между напряжением на входе и напряжением на входе.
называется постоянной фазы и показывает сдвиг фаз между напряжением на входе и напряжением на входе.
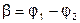
Эквивалентные схемы можно построить на основе уравнений четырехполюсника, записанных в Z -, Y- и H -формах. Поскольку четырехполюсник в общем случае описывается четырьмя независимыми параметрами, то каждая такая схема будет содержать четыре элемента. Так как Z -уравнения выражают напряжения на зажимах как сумму двух слагаемых, пропорциональных токам, то в схеме замещения имеем последовательное соединение сопротивлений и управляемых источников ЭДС (рис. 12.2, а).
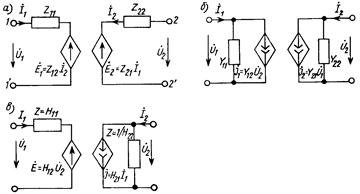
Рис. 12.2
Аналогично Y -уравнения приводят к схеме рис. 12.2, б, реализующей принцип суммирования токов в параллельных ветвях, содержащих проводимости и управляемые источники тока. Подобным же образом строится схема замещения (рис. 12.2, в), отвечающая гибридным уравнениям.
На рис. 12.2, а-в изображены двухгенераторные эквивалентные схемы, каждая из них содержит два управляемых источника. На рис. 12.3, а, б показаны одногенераторные схемы, включающие лишь по одному управляемому источнику.
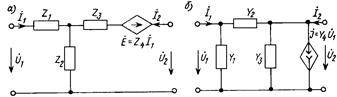
Рис. 12.3
Для входного и выходного напряжений Т-образной схемы рис. 12.3, а имеем:
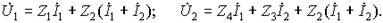
Сопоставляя эти уравнения с Z -уравнениями четырехполюсника (12.1), получим условия их эквивалентности:
Z 1 + Z 2 = Z 11; Z 2 = Z 12;
Z 4 + Z 2 = Z 21; Z 3 + Z 2 = Z 22,
из которых найдем выражения для параметров Т-образной схемы через Z -параметры четырехполюсника:
Z 1 = Z 11 – Z 12; Z 2 = Z 12;
Z 3 = Z 22 – Z 12; Z 4 = Z 21 – Z 12.
Аналогично параметры одногенераторной П-образной схемы (рис. 12.3, б) можно выразить через Y -параметры. Ее входной и выходной токи равны
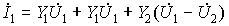 ;
; 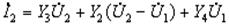 .
.
Эквивалентность этих уравнений Y -уравнениям четырехполюсника (12.2) обеспечивается при:
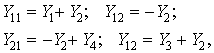
откуда получаем выражения для параметров П-образной схемы (рис. 12.3, б) через Y -параметры четырехполюсника:
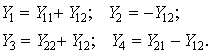
 2015-03-27
2015-03-27 2760
2760








