1) Область определения функции: 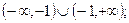 пересечение оси 0х в точке (1;0), а оси 0у - (0;-1);
пересечение оси 0х в точке (1;0), а оси 0у - (0;-1); 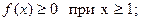
2) 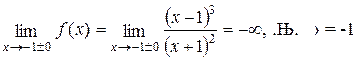 точка разрыва;
точка разрыва;
3) Из 2) следует, что 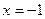 вертикальная асимптота;
вертикальная асимптота;
Находим наклонную асимптоту:
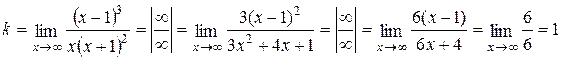
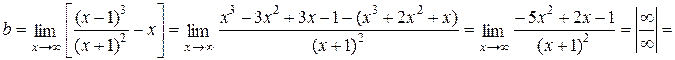
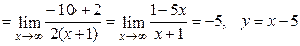 – наклонная асимптота при
– наклонная асимптота при 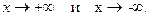
4) 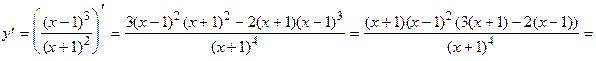 =
= 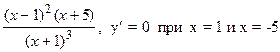
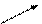 при
при 
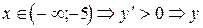 (возрастает)
(возрастает)

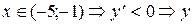 (убывает)
(убывает)

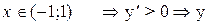 (возрастает)
(возрастает)

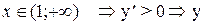 (возрастает)
(возрастает)
5) Из предыдущего 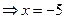 точка максимума,
точка максимума,
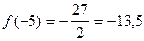 - max;
- max;
6) 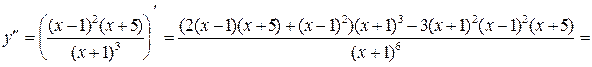
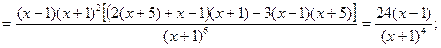
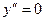 при
при 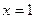 ;
;









 При
При 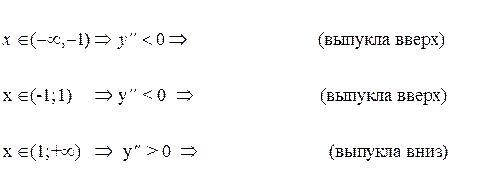
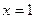 абсцисса точки перегиба,
абсцисса точки перегиба, 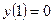 .
.
Результаты исследования внесем в следующую таблицу
| х | 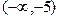
| -5 | (-5;-1) | (-1;1) | (1;+4) | |
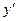
| + | - | + | + | ||
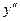
| - | - | - | - | + | |
| y | 
| -27/2- max |
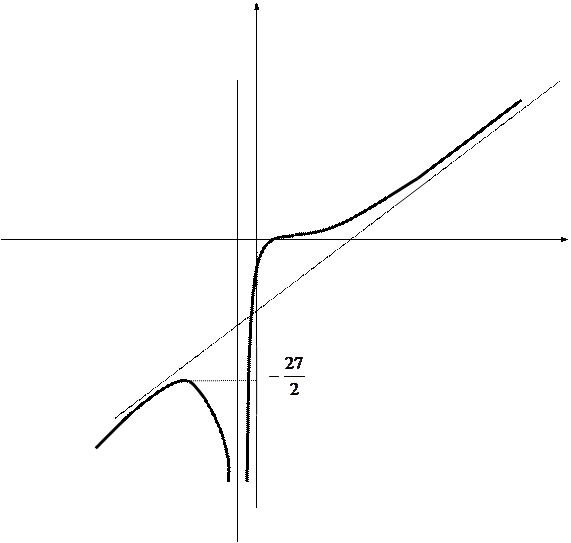

Задача 12. Дана функция 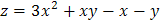 и две точки
и две точки 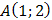 и
и 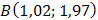 . Требуется:
. Требуется:
1) вычислить значение 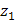 в точке
в точке 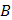 ;
;
2) вычислить приближенное значение функции 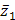 в точке
в точке 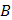 , исходя из значения
, исходя из значения 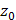 функции в точке
функции в точке 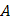 и, заменив приращение функции при переходе от точки
и, заменив приращение функции при переходе от точки 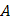 к точке
к точке 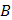 дифференциалом;
дифференциалом;
3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом;
4) составить уравнение касательной плоскости к поверхности
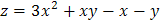 в точке
в точке 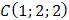 .
.
 2015-03-07
2015-03-07 588
588








